機械学習は、機械自身がビッグデータから知識を抽出し学ぶことである。機械が学ぶために用いられるデータは、訓練データと呼ばれている。機械学習は、訓練データの特徴に応じて、大まかに教師あり学習と教師なし学習とに分けることができる。特徴量と教師ラベルを同時に持つ訓練データを使用して学習する場合は、教師あり学習という。また、特徴量のみからなる訓練データを使用して学習する場合は、教師なし学習という。一部の特徴量に対して教師ラベルが存在し、そのほかの一部の特徴量に対して教師ラベルが存在しないような訓練データを使用して学習する場合は、半教師あり学習という。そのほかに、これらと少し異なるタイプの機械学習として、強化学習というものが存在する

教師あり学習
教師あり学習(supervised learning)は、教師ラベル付きの特徴量からなる訓練データを用いた機械学習である。訓練データには、観測されたデータだけでなく、そのデータの「答え」に相当するラベル情報も含まれている。例えば、画像分類の場合は、画像が観測データにあたり、その画像に写っているオブジェクト(犬・猫など)が教師ラベルとなる。特徴量と教師ラベルをセットで学習することにより、機械は大量な特徴量データの中から、各ラベルに特異的なパターンを見出して学習できるようになる。
教師あり学習は、分類(判別)問題と回帰問題に応用できる。分類問題は、犬・猫などのカテゴリー変数を予測する問題であり、回帰問題は、穀物の収量などの連続した実数値を予測する問題である。
分類問題
分類問題(判別問題)は、与えられた特徴から、それがどのカテゴリに属しているのかを予測する問題である。この際に、訓練データとして、各カテゴリとそのカテゴリに属しいているサンプルの特徴量を同時に機械に学習させる。
円形と三角形を分類する例を考える。次の図をみると、円形と三角形の違いを区別するためには、色に着目するのが良さそう。ここで、白なら 1.0、黒なら 0.0 となるように色を数値化して特徴 1(x1)とする。白い円も存在することから、特徴 1 だけでは不十分と考えられる。そこで、図形の面積とその外接円の面積との比率を特徴 2 (x2)としてみる。円とその外接円の面積はほぼ同じであるからその比率は 1.0 に近い。これに対して、三角形の面積は、その外接円の面積よりも小さく、その比率は 1.0 よりも小さい。このように特徴 1 と特徴 2 を調べて、両者を平面座標に表示することで、円と三角形を分ける線を引くことができる。両者を分けるための線の引き方は様々である。その線の引き方が分類アルゴリズムである。

回帰問題
訓練データの教師ラベルが連続値である場合、回帰問題と呼ぶ。例えば、施肥量が多くなると小麦の収量が増えることが一般的に知られていて、そこで両者の関係を調べ、施肥量(x1)を使用して、その年の小麦の収量(y)を予測したい場合などが回帰問題になります。特徴量(施肥量)と教師ラベル(収量)を同時に与えることで、機械は両者の間に隠された相関関係を見出して、数式化する(モデルを構築する)。そして、この数式を用いて、将来の入力に基づいて予測を行う。回帰問題の場合、教師ラベルを応答変数や目的変数など呼ぶことが多い。また、特徴量を予測変数や説明変数と呼ぶことが多い。

学習アルゴリズム
教師あり学習で使われるアルゴリズムには以下のようなものがある。これらのアルゴリズムは、すべて訓練データからパターンを導くものである。そのため、これらのデータで作られたモデルを予測に使用するには、入力となるデータも訓練データと同じ条件下で取る必要がある。したがって、多様な条件下でバラエティのある訓練データを収集して学習するのが、高い汎化性能の構築に必要不可欠なことである。
| 回帰 | 回帰問題 | 既知のデータを線形回帰し、その係数を求める。次に、これらの係数を利用して、未知のデータに対して、数値予測を行う。 |
| 時系列解析 | 回帰問題 | 過去の値を利用して、未来の値を予測する方法。 |
| k 近傍法 | 分類問題 | 未知のデータに対して、k 個の学習データのうち、最も近いものを選ぶというアルゴリズムである。 |
| SVM | 分類問題・回帰問題 | 少ないデータでもより正確に分類できる統計的機械学習アルゴリズムの一つである。回帰問題を解くサポートベクター回帰(SVR)もある。回帰問題との区別を明確にするために、分類問題の場合は SVC と書かれることもある。 |
| 決定木 | 分類問題・回帰問題 | 閾値を設けて、与えられたデータをその閾値と比較して 2 つのグループに分ける。グループに分けた後、さらにその下で 2 つのグループをわける。分類問題を解くときの分類木と回帰問題を解くときの回帰木がある。 |
| ランダムフォレスト | 分類問題・回帰問題 | 決定木を大量に生成し、各決定木の結果を統合的に検討し、予測する手法。決定木と同じく判別問題と回帰問題の両方に適用できる。 |
| ニューラルネットワーク | 分類問題・回帰問題 | 複数のパーセプトロンを繋げて構築したニューラルネットワークで学習を進める方法。パラメーター数が多くなりがちのため、訓練データを大量に用意できる場合に有効である。 |
教師なし学習
教師なし学習は、特徴量のみからなる訓練データを用いた機械学習である。教師ラベルは存在しないので、機械は、大量なデータを読み解き、機械自身がデータに隠された特徴やパターンを抽出することになる。そして、機械は、抽出した特徴やパターンに応じて、それらの大量なデータをいくつかのグループに分けたり(クラスタリング)、あるいは、これらの特徴やパターンを表すのに有効な新しい変数(特徴抽出・次元削減)を見つけたりする。
クラスタリング
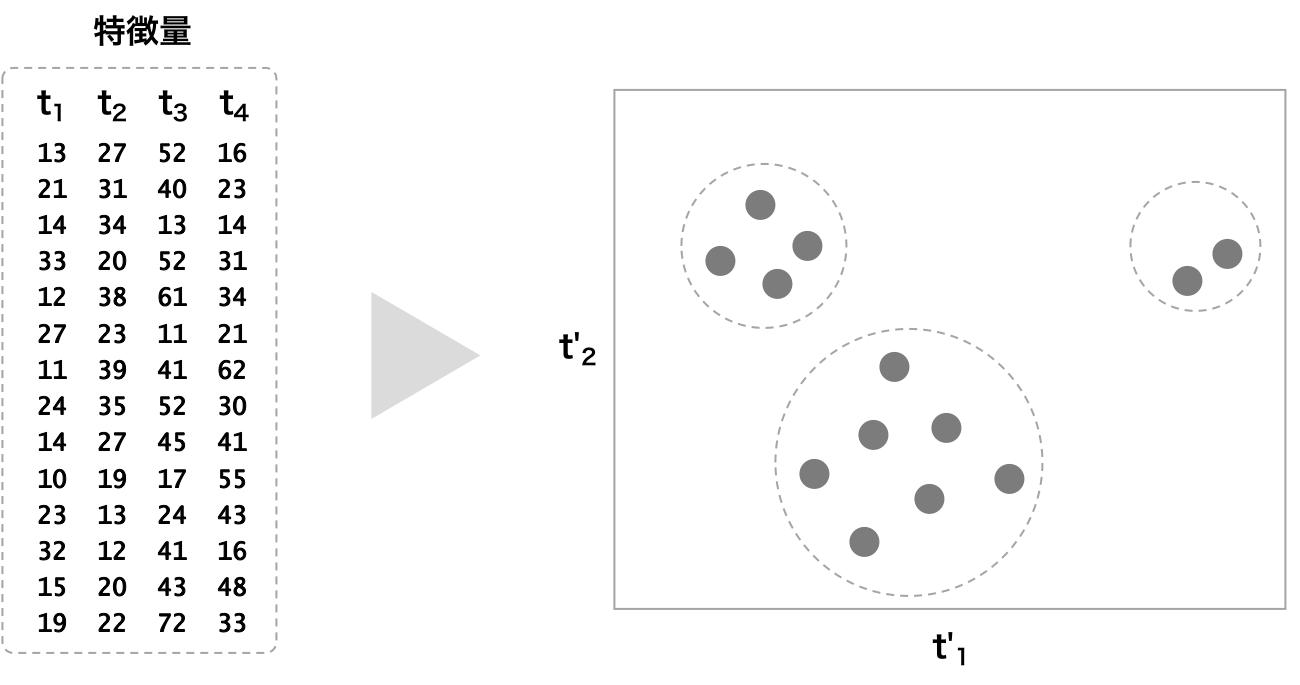
サンプル同士が似ていることは、両者の特徴が似ているということである。似たサンプル同士を一つのグループに取りまとめる場合、サンプル同士の特徴量の距離に着目し、距離の近いサンプル同士をまとめればよい。このように、特徴量の距離の近いもの同士を集めていくことをクラスタリングという。クラスタリングアルゴリズムは、階層構造の有無によって、非階層的クラスタリングおよび階層的クラスタリングに分けることができる。
非階層的クラスタリングでは、データの特徴を調べて、特徴の似たデータ同士を集めてクラスタを作る方法である。代表的なアルゴリズムとして k-means などがある。
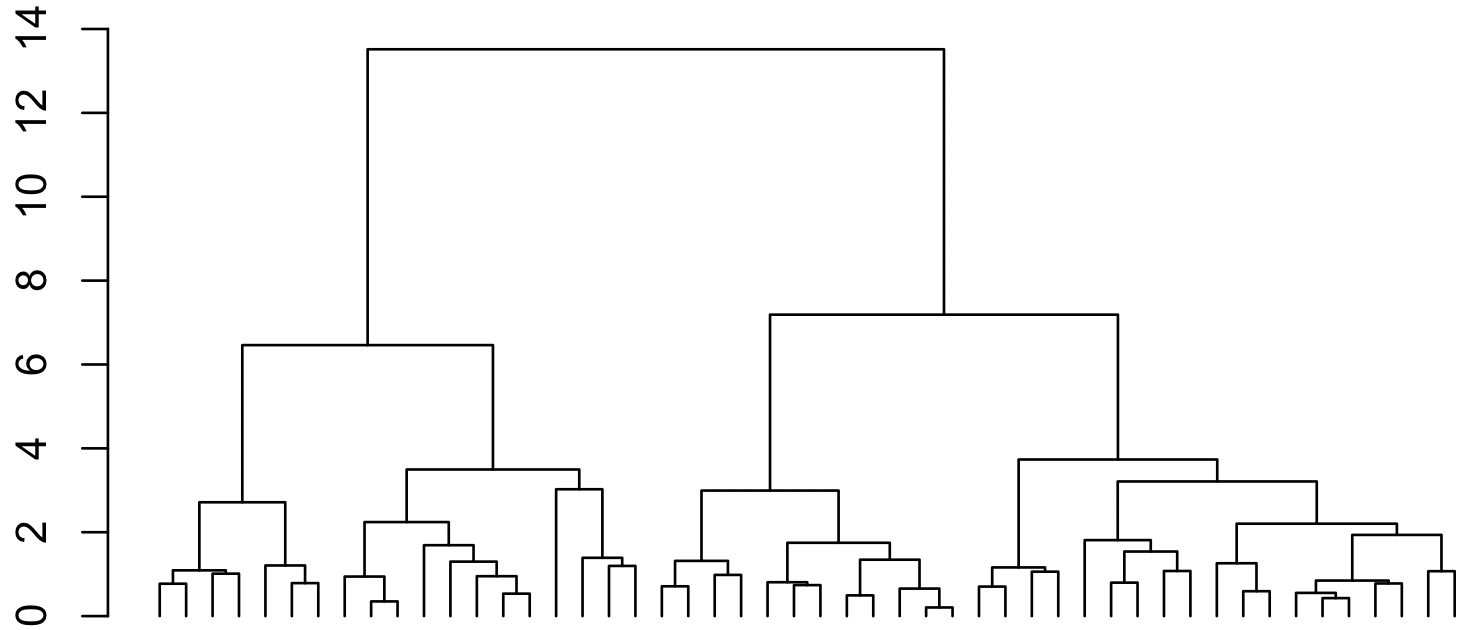
階層的クラスタリングには、凝集型と分割型がある。凝集型では、1 つのデータを 1 つのクラスタとして、クラスタ同士を順次に併合していくことで階層的なクラスタを作り上げる方法である。凝集型の階層的クラスタリング手法には、群平均法、最短距離法、最長距離法やウォード法などがある。分割型では、DIANA (DIvisive ANAlysis Clustering) アルゴリズムの考え方が中心となったクラスタリング手法で、すべてのデータを 1 つのクラスタとして順次にクラスタを細かく分割していくことで階層的なクラスタを作り上げる方法である。
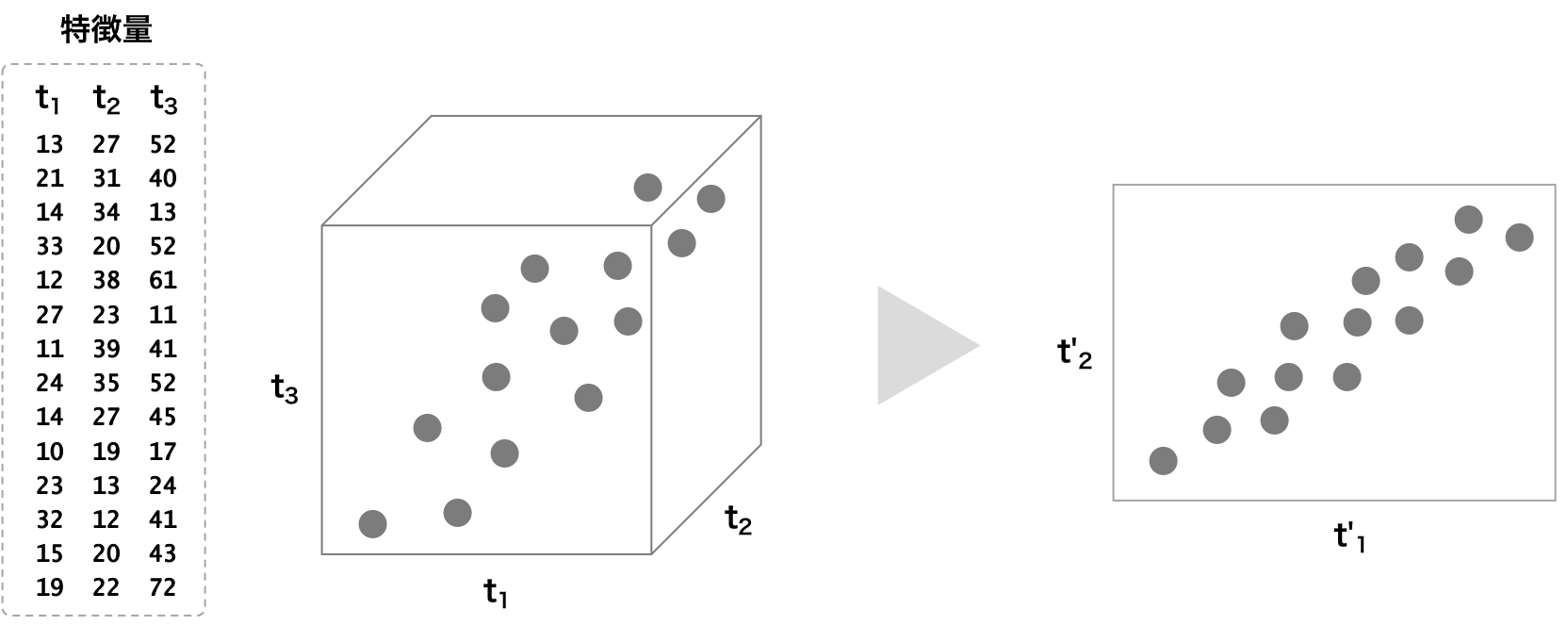
特徴抽出・次元削減
ビッグデータの多くの場合は高次元である。このような高次元のデータの中に、重要な情報が含まれるほかに、ノイズや相関の高い情報が複数含まれている場合が多い。このような高次元データに対して、次元数を減らすことで、ノイズが軽くなったり、相関の高い情報が 1 つにまとまったりするようになる。教師なし機械学習は、高次元データに対して、特徴抽出や次元削減にも使われている。特徴抽出・次元削減の方法として、主成分分析(PCA)などがある。