pLSI はトピックモデルにおいて、確率計算に基づいてトピックを推定する方法である。pLSI は、ある単語 w が文書 d に含まれるとき、その生成確率 p(w,d) を最大にするトピックを推定している。文書 d 中に単語 w が生成される確率 p(w,d) は、文書全体の中から文書 d を選ぶ確率 p(d) と文書 d 中に現れる単語 w の確率 p(w|d) の積によって表せる。一般に、p(d) は、全文書の中から文書 d を選ぶ確率なので、一般に多項分布に従う変数とする。
\[ p(w, d) = p(d)p(w|d) \]文書 d が与えられたとき、その文書から生成されるトピックが k である確率を p(k|d) とおく。また、トピック k が与えられたとき、そのトピックから生成される単語が w である確率を p(w|k) とおく。このとき、文書 d 中に単語 w が生成される確率 p(w,d) は次のように書ける。
\[ p(w, d) = p(d)p(w|d) = p(d) \sum_{k=1}^{K}p(w|k)p(k|d) \]いま、W 行 D 列からなる行列 X が与えられたとする。行列 X の (w,d) の成分 xwd を文書 d 中における単語 w がの TF-IDF スコアとする。このとき、データ全体における対数尤度は次のように計算できる。
\[ \begin{eqnarray} L &=& \sum_{d=1}^{D}\sum_{w=1}^{W}x_{wd}\log p(w, d) \\ &=& \sum_{d=1}^{D}\sum_{w=1}^{W}x_{wd}\log \sum_{k=1}^{K}p(w|k)p(k|d)p(d) \end{eqnarray} \]この対数尤度を最大化することは、データから計算された \(p(w|d)\) とモデルから計算された \( \sum_{k=[1}^{K}p(w|k)p(k|d) \) のカルバック・ライブラー情報量を最小化にすることと等しい。pLSI では、EM アルゴリズムを利用してカルバック・ライブラー情報量の最小化を行なっている。
LSI と pLSI の関係
文書とトピックの関係および単語とトピックの関係は、同じようにモデル化される。つまり、文書からトピックを生成する確率は、トピックから文書を生成する確率と同じと考えることができる。このとき、確率 p(w,d) は次のように書き表すこともできる。
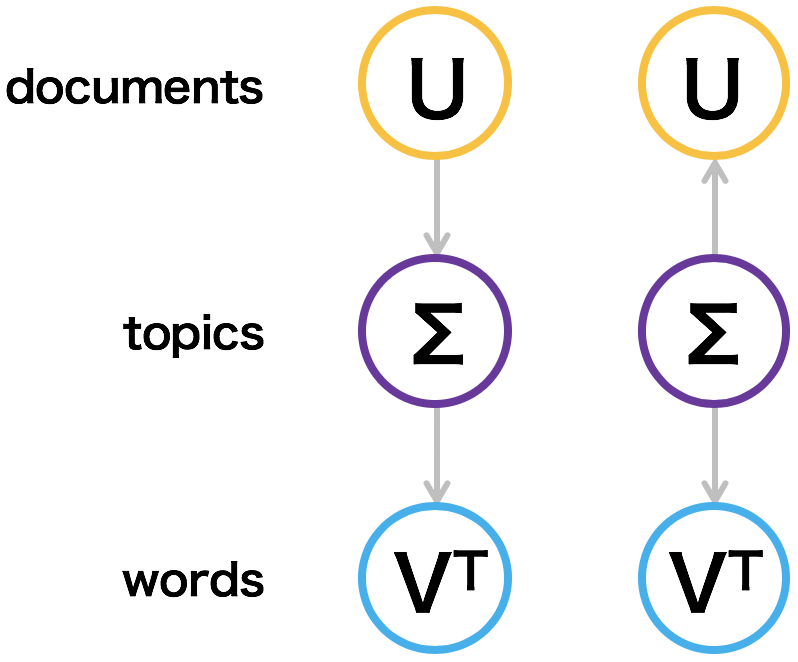
\[ p(w,d) = \sum_{k=1}^{K}p(k)p(d|k)p(w|k) \]両者をグラフィカルに表すと、次図のようになる。文書と単語の出現頻度表 X が与えられたとき、LSI アルゴリズムにより特異値分解を行ってトピックを求めることができる。このとき X は、X = UΣVT のように 3 つの行列に分解できる。これら 3 つの行列 Σ, U, V と p(k)、p(d|k)、および p(w|k) を見比べると、3 者それぞれが対応していることがわかる。pLSI が LSI の確率的なアプローチと言われているのはこのことに由来する。