LSI (Latent Semantic Indexing) は、行列の特異値分解(SVD)に基づくトピックを推定する手法の一つである。一般に、任意の行列 X は、対角行列 Σ とすると、X = UΣVT のように 2 つの直行行列 U と V に分解できることが知られている。
\[ X = U\Sigma V^{T} = U \begin{pmatrix} \hat{\sigma}_{1} & & O \\ & \ddots & \\ O & & \hat{\sigma}_{r} \\ \end{pmatrix} V \]特異値分解によって求められた対角行列 Σ の各要素を特異値とよぶ。これらの特異値を σ1 ≥ σ2 ≥ ... ≥ σr のように並び替えることができる。また、対角行列 Σ のランクは、行列 X のランク r と一致する。対角行列 Σ は一意的に求められるが、直行行列 U と V は複数存在する可能性がある。
ここで、X を v 行 d 列の行列とする。行列 X の (v, d) 要素を、文書 d 中に出現した単語 v の出現頻度あるいは TF-IDF スコアとする。すると、この行列 X は、X = UΣVT のように分解できる。このとき、直行行列 U は、v 行 r 列の行列となり、各行はトピックに対する単語のベクトルの表現となっている。また、直行行列 V は、d 行 r 列の行列となり、各行はトピックに対する文書のベクトル表現となっている。
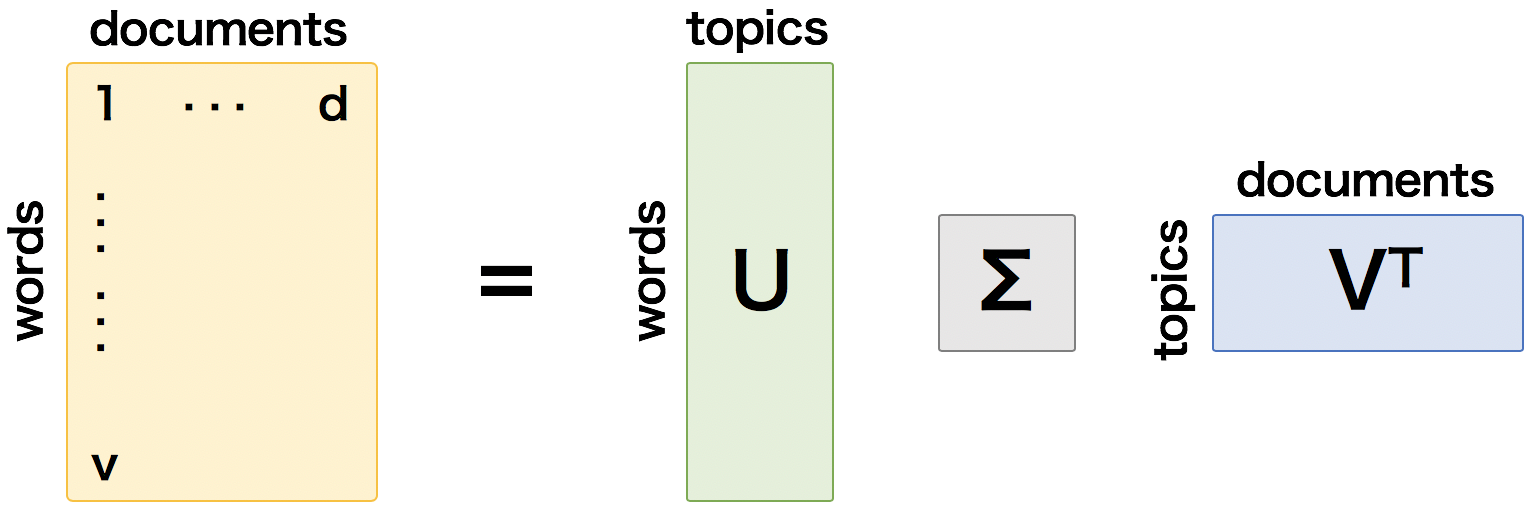
このとき、与えられた文書を k 個のトピックに分類したいとき、X の特異値分解により得られた特異値を大きいものから k 個とそれに対応する行列 U と V を選べばよい。
\[ \hat{X} = \hat{U}\hat{\Sigma} \hat{V}^{T} = \begin{pmatrix} \hat{\mathbf{U}}_{1} & \hat{\mathbf{U}}_{2} & \cdots & \hat{\mathbf{U}}_{k} \\ \end{pmatrix} \begin{pmatrix} \hat{\sigma}_{1} & & O \\ & \ddots & \\ O & & \hat{\sigma}_{k} \\ \end{pmatrix} \begin{pmatrix} \hat{\mathbf{V}}_{1}^{T} \\ \hat{\mathbf{V}}_{2}^{T} \\ \vdots \\ \hat{\mathbf{V}}_{k}^{T} \\ \end{pmatrix} \]