LDA (Latent Dirichlet Allocation) は、pLSI と同様に確率的なアプローチにより、トピックを推定するアルゴリズムとなっている。pLSI は、尤度最大化のよるトピック推定を行うのに対して、LDA はベイズ推定によるトピック推定を行なっている。
ある単語 w が文書 d に含まれるとき、その生成確率 p(w,d) を考える。ここで、p(w, d) は、文書 d が与えられたとき、トピックが k になる確率を p(k|d) とおく。また、トピック k が与えられたとき、単語が w になる確率を p(w|k) とおく。このとき、p(w, d) は次のように書き表すことができる。
\[ p(w, d) = p(d)p(w|d) = p(d) \sum_{k=1}^{K}p(w|k)p(k|d) \]pLSI では、p(w, d) の尤度が最大にするような p(w|k) と p(k|d) を、EM アルゴリズムにより推定している。これに対して、LDA では階層ベイズモデルを導入し、p(w|k) および p(k|d) が多項分布に従うものとしてベイズ推定を行なっている。
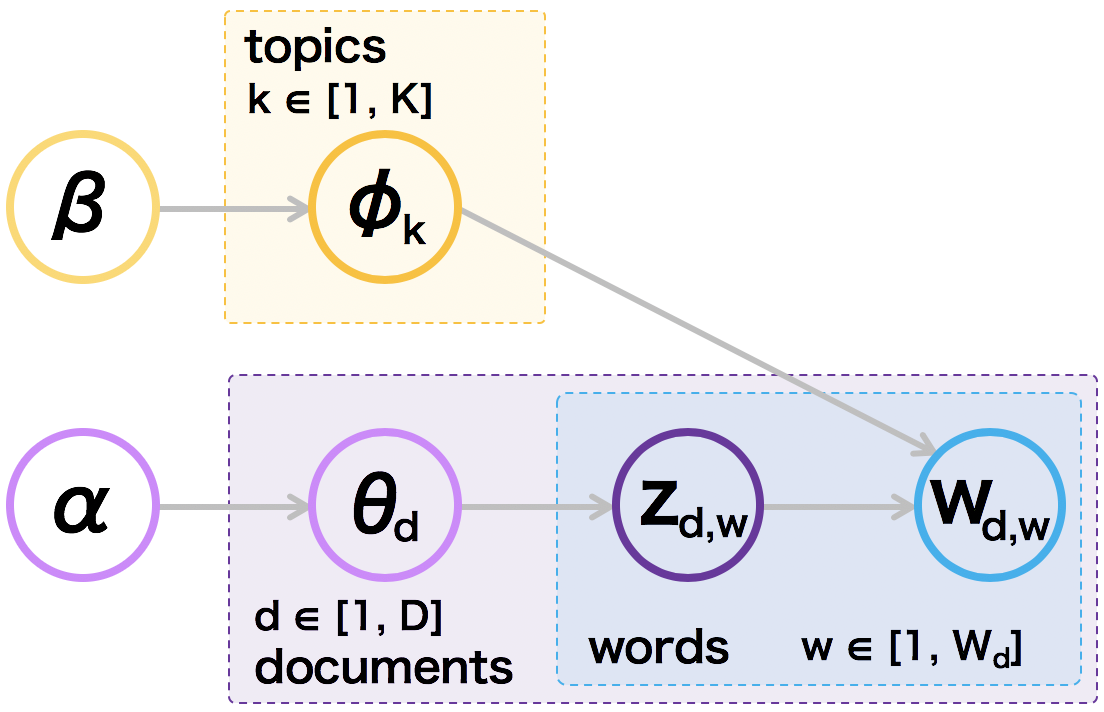
まず、p(w|k) に関しては、単語 w がトピック k の確率分布 φk から生成されると考える。φk は、パラメーター β を持つディリクレ分布に従うものとする。次に、p(k|d) に関して、文書 d に各トピックが含まれる確率分布を θd とする。θd は、パラメーター α を持つディリクレ分布に従うものとする。また、文書 d に含まれている、各トピックの単語 w の確率分布を zd,w とする。このとき、パラメーター α と β が与えられた時の同時確率分布は次のように書ける。
\[ p(\theta_{d}, z_{d,w}, \phi_{k}|\alpha, \beta) = p(w|z_{d,w}, \phi_{k})p(z_{d,n}|\theta_{d})p(\theta_{d}|\alpha)p(\phi_{k}|\beta) \]