トピックモデルは、文書中に出現している単語の種類と出現頻度に基づいて、その文書の潜在的な意味（トピック）を解析する手法の一つである。文書に対して主成分分析を行い、その文書を構成している主成分（トピック）を抽出するようなイメージである。あるいは、文書に対してクラスタリングを行うようなイメージである。このようにトピックモデルは、主成分分析やクラスタリングと似たもので、教師なし学習として分類される。

単語の出現頻度

トピックモデルを適用するには、各文書における単語の出現頻度表を作成することから始める。まず、文書を分解して得られた単語の集合から、無意味な文字列や記号、分類にほとんど関与しないと思われる単語を除去する。続いて、単語の活用形を統一させる。動詞ならば、現在進行形・過去形・過去分詞を原形に揃えたり、名詞ならばすべて単数形に揃えたりする。その後、整形後の各単語の、各文書中で出現している回数を数えて、出現頻度表を作成する。すべての文書に出現している単語や数回しか出現しなかった単語は、文書の分類にほとんど関与しないと思われるので、このような単語を除去する。

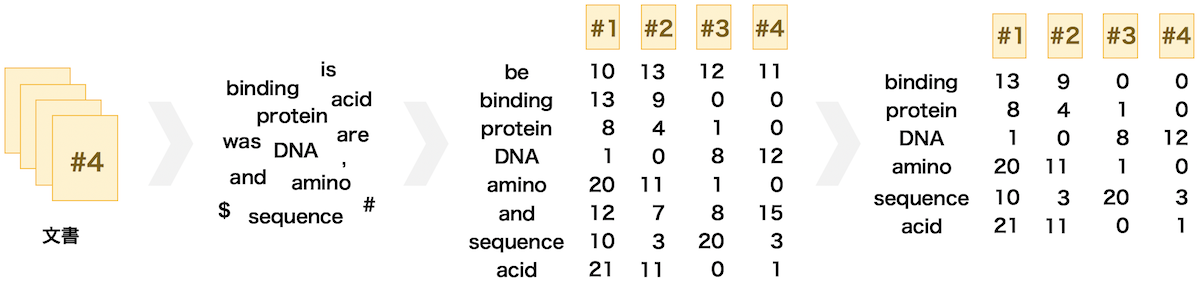
BoW (bag-of-words)

BoW は文書中の単語を表現する方法の一つである。各文書中の単語の出現頻度をベクトルで表したものである。ベクトルの各要素には順序関係がない。文書が長いと、単語の種類も多くなる。そのため、その文書の単語を BoW 表現で表そうとすると、非常に大きな次元を持ったベクトルを必要とする。また、文書が増えることで、単語の種類がさらに増える。複数の文書の BoW 表現のベクトルをまとめて、行列として見たとき、その行列がスパース（0 の要素が多い）になることが多い。

n-gram

文書を分解して単語の集合を作るとき、1 つ 1 つの単語を文書の構成要素とみなすことができる。この他に、複数の単語を 1 単位の構成要素とみなすこともできる。n 個の単語を 1 単位として扱うときこれを n-gram 表現という。例えば、「To consult the statistician after an experiment is finished is often merely to ask him to conduct a post mortem examination.」を 3-gram 表現で表すと、to consult the、consult the statistician、the statistician after、・・・、a post mortem、post mortem examination のように表せる。

n は解析の目的やデータの特徴に応じて決める。特に、根拠を持てないような場合については、いくつかの n を試して、性能がもっともよかった時の n を選択する。

ストップワード

文書のデータを処理するにあたって、どの文書にも普遍的に現れているような単語をストップワードという。例えば、is、a、the、and などがストップワードである。ストップワードは、文書を分類する上で、有益な情報を含んでいないため、解析の前処理として、除去するすべきである。

モデル構築

単語の出現頻度をそのまま使うと文書をうまく分類できない場合がある。これは、すべての文書に共通して高頻度で出現する単語がある場合、その単語にウェイトがかかり、分類の性能が悪くなるからである。より高い分類性能を得るためには、すべての文書に共通して出現する単語の重要度を減らしたり、一部の文書だけに出現する単語の重要度を増やしたりする処理を行う必要がある。そのため、より性能の高い分類モデルを作るには、単語の出現頻度をそのまま使わずに、その出現頻度から計算された重要度を使った方がいい。この重要度として Term Frequency-Inverse Document Frequency (TF-IDF) スコアが使われる。一度、TF-IDF スコアを計算できれば、このスコアに対して様々な処理を行い、トピック推定を行う。

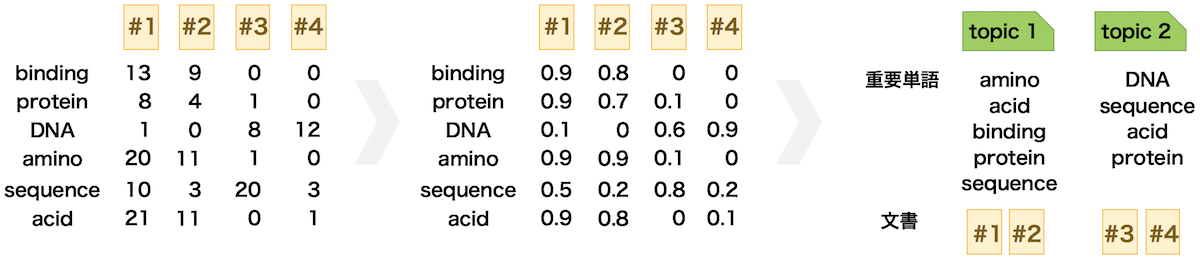
TF-IDF スコア

すべての文書に頻出する単語は、文書を分類する上で役に立たないことがある。逆に、一部の文書だけに頻出単語であれば、文書を分類する上で役に立つことが容易に想定できる。モデルを構築するときに、このようなことを考慮すると性能の良いモデルを作成できる場合が多い。

TF-IDF と呼ばれる方法を使用することで、各単語の出現頻度に応じてその重要度を計算することができる。この方法では、文書 t 中の単語 d の出現頻度を tf(t, d) と表し、文書 t 中の単語 d の逆文書頻度を idf(t, d) とすると、その単語の TF-IDF スコアは、次のように計算される。

逆文書頻度 idf(t, d) は、文書の総数を n とおくと、次のように定義されている。ただし、この定義には何種類か存在するので、機械学習フレームワークを使って計算するときに少し注意を払う必要がある。

計算アルゴリズム

トピックを推定するアルゴリズムとして、特異値分解（SVD）に基づく方法（下図の上部分）と確率計算に基づく方法（下図の下部分）がある。SVD に基づく方法には Latent Semantic Index (LSI) があり、確率計算に基づく方法には Probabilistic Latent Semantic Indexing (pLSI) や Latent Dirichlet Allocation (LDA) などがある。

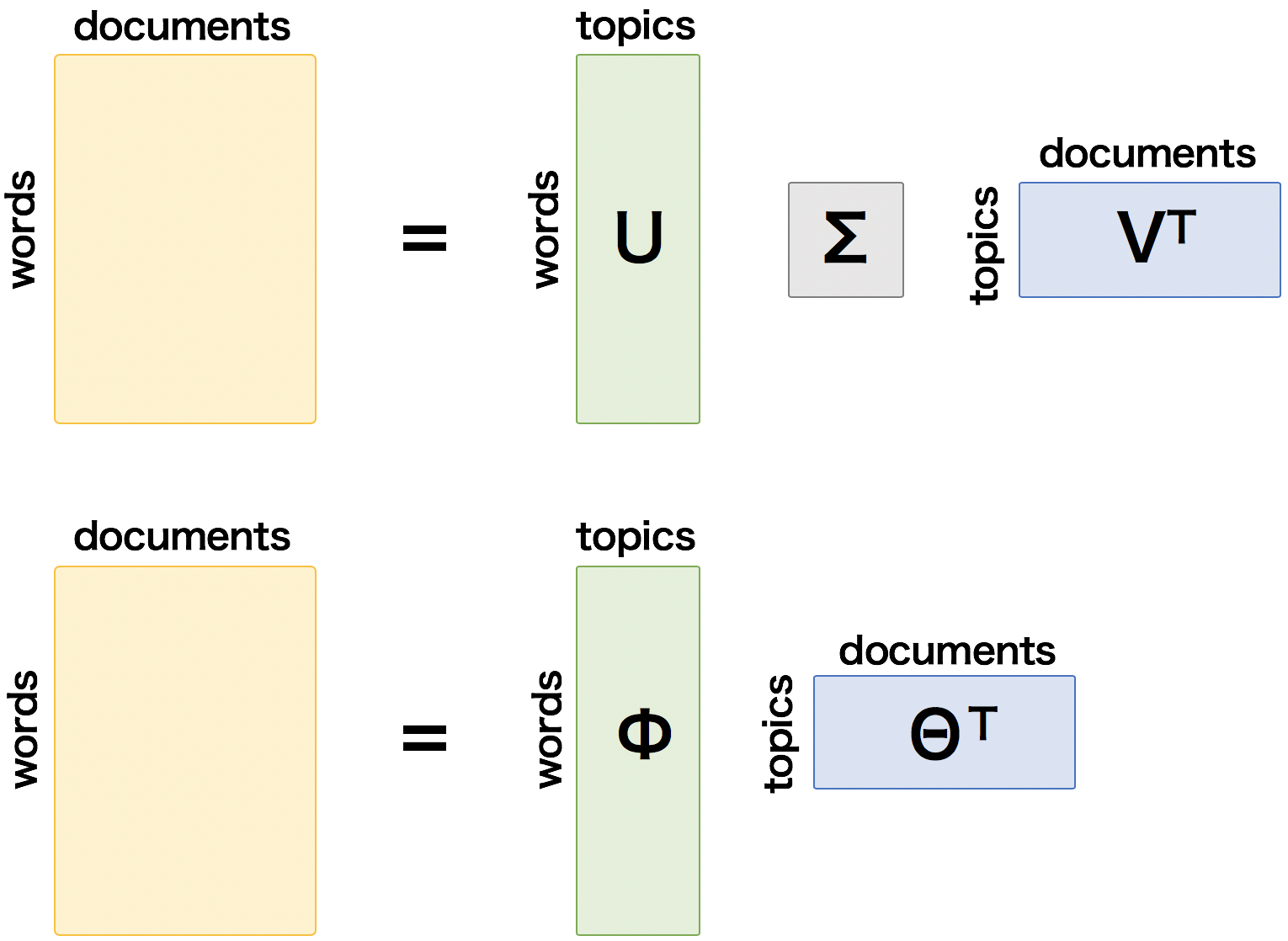
LSI は、行列の特異値分解（SVD）を使用した方法である。一般に、任意の行列 A は、A = UΣV^T のように分解されることが知られている。ここで、m 個の文書と n 個の単語からなる単語の出現頻度あるいは TF-IDF スコアを行列 A としたとき、行列 A は UΣV^T に分解される。A の各列が文書、各行が単語を表すとすると、行列 U と行列 V は z 列からなり、z 個のトピックを表す。また、行列 U の各行はトピックに関する単語ベクトルの表現であり、行列 V の各行はトピックに関する文書ベクトルの表現である。

pLSI は、特異値分解の代わりに確率的なアプローチでトピック推定を行う方法である。pLSI では、文書 d に単語 w が含まれる確率を p(d, w) としたとき、すべての文書と単語における同時確率 p(D, W) が最大となるようにトピックを決める。文書が d のとき、トピックが z であるときの確率は p(z|d) と書ける。また、トピックが z のとき、単語が w となる確率は p(w|z) と表せる。このとき、p(D, W) は次のように表せる。p(D) はデータが与えられると計算できる。このとき、p(Z|D) と p(W|Z) を EM アルゴリズムにより推測できる。

LDA は、pLSI の確率計算にベイジアン推定を導入して計算を行う方法である。このとき、パラメーターの事前分布としてディリクレ分布を用いる。

様々なトピックモデル

LSI、pLSI や LDA の他に、LDA をさらに拡張した方法が多数報告されている。例えば、hierarchical LDA (hLDA) は、データの中からトピックの階層性を推定するアルゴリズムとして知られている。同様に、pachinko allocation model (PAM) も階層性トピックモデルの一つで、階層性を推定するときに有向非巡回グラフを用いている。さらにhLDA をベイジアンモデルを導入したりするなどの方法が報告されている。

階層性トピックモデルの他に相関トピックモデル（Correlated Topic Model; CTM）も報告されている。トピックモデルや階層性トピックモデルにおいて、トピック同士は互いに独立であることを仮定しているのに対して、CTM では 2 トピック同士が相関していることを想定したモデルである。

生物学への応用

トピックモデルは自然言語処理向けに考え出された手法であるが、近年では生物学データの解析に取り入れるようになった。トピックモデルは、生物データや医療データに対するテキストマイニングのほか、とくに分類やクラスタリングの手法として使われる場合が多い（Liu et al., 2016）。この場合、一般的なクラスタリングと異なり、1 つのサンプルを複数のクラスタに分けることができる。

トピックモデルがマイクロアレイの遺伝子発現量行列をクラスタリングするために用いられている研究が、報告されている（Rogers et al., 2005, Masada et al., 2009）。これらの研究では、各サンプルを文書とみなし、各遺伝子を文書中に出現している単語とみなして、クラスタリングを行なっている。また、遺伝子発現量行列をクラスタリングし、遺伝子制御ネットワークを同定する研究も行われている（Coelho et al., 2010）。

また、トピックモデルは、生物種に特有な塩基配列パターンの検出にも使われている。この場合、ゲノムを文書とみなし、その塩基配列を k-mer に分解したデータを単語とみなして解析を行なっている（Chen et al., 2010）。