SVM は分類問題を解く機械学習手法の一つである。SVM では、データを分類するための超平面を求めて、その超平面を用いてデータの分類を行なっている。その超平面を計算する方法としてハードマージン法とソフトマージン法がある。ハードマージン法は、データが空間上できれいにクラスごとに分離している場合だけに適用できる。これに対して、ソフトマージン法は、データがきれいに分離していなくても適用でき、その適用範囲は広い。ソフトマージン法では、教師データが間違って分類された場合に、ペナルティを与えることで誤分類に対応している。
ソフトマージン法の定式化
マージン最大化
ソフトマージン法は、ハードマージン法と同様に定式化することができる。すなわち、マージンを最大化することは、次式の右辺を最大化する問題に帰着できる。
\[ \frac{\mathbf{w}^{t}(\mathbf{x}_{positive} - \mathbf{x}_{negative})}{||\mathbf{w}||} = \frac{2}{||\mathbf{w}||} \]制約条件
2/||w|| の最大化は、制約条件のもとで行わなければならない。ハードマージン法では、2 つのサポート超平面の間にサンプルが存在しないことを利用して、制約条件を次のようなものとしている。
\[ y^{(i)}( w_{0} + \mathbf{w}^{t}\mathbf{x}^{(i)}) \ge 1 \]これに対して、ソフトマージン法では、あるクラスに属するサンプルが、サポート超平面(g(x) = -1 または g(x) = 1)を超えて他のクラスの近くに配置されていることも許している。ただし、この場合は、ペナルティを課す。例えば、下図のように、円形のサンプル 1 がサポート超平面 g(x) = -1 を超えて、三角形のクラスタの中に配置されている。このとき、サンプル 1 が、自分側のサポート超平面から誤分類された位置までの距離 ξ1/||w|| をペナルティとして課す。また、サンプル 2 にように、自分側のサポート超平面 g(x) = -1 を超えているが、分離超平面 g(x) = 0 を超えていないような点についても同様にペナルティを課す。
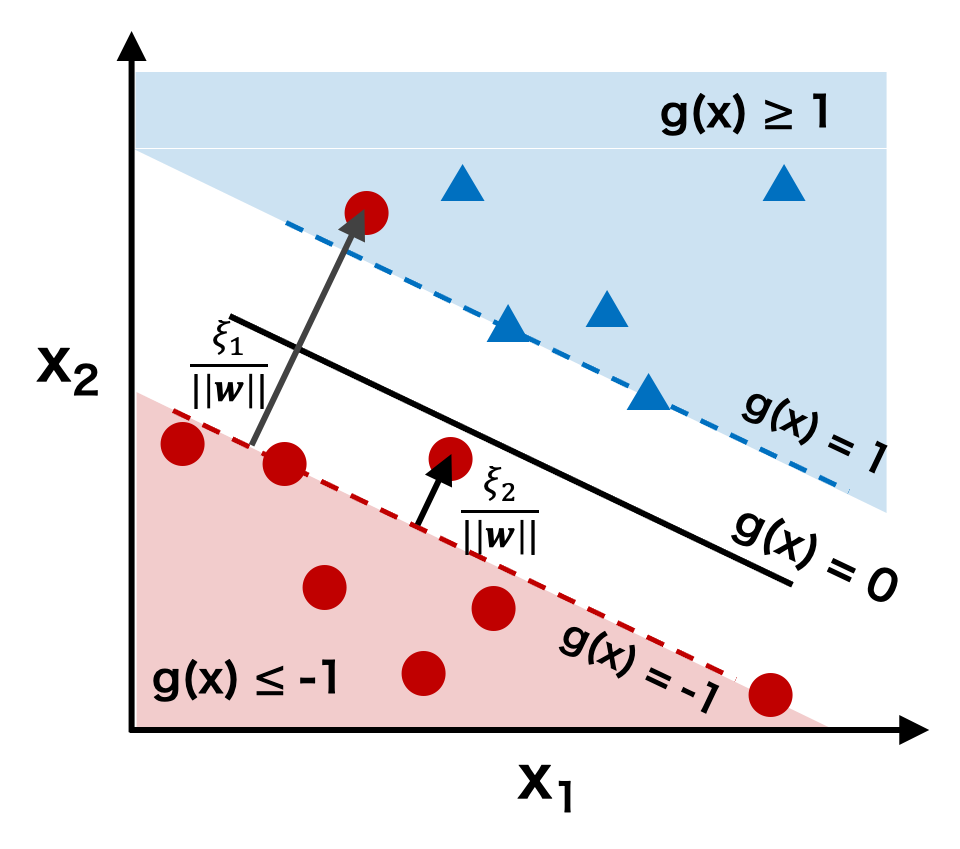
このペナルティを、ハードマージン法の制約条件に取り入れると、次式が得られる。これがソフトマージン法の制約条件の基本となる。
\[ y^{(i)}( w_{0} + \mathbf{w}^{t}\mathbf{x}^{(i)}) \ge 1 - \frac{\xi_{i}}{||\mathbf{w}||} \quad \xi_{i} \ge 0\]ξi については、サンプル i が自分側のサポート超平面以内であれば ξi = 0 であり、サポート超平面を超えて向こう側に存在していれば ξi > 0 である。そのため、サポート超平面(g(x) = -1 または g(x) = 1)と分離超平面の距離(g(x) = 0)の距離を考えたとき、サンプル i がサポート超平面と分類超平面の間であれば、0 < ξi/||w|| < 1 であり、分離超平面を超えた誤分類であれば ξi/||w|| > 1 になる。
ここで、すべての点のペナルティについて考えると、このペナルティは次のように書ける。
\[ \sum_{i=1}^{n}\frac{\xi_{i}}{||\mathbf{w}||} \]サポート超平面を超えていないサンプル i については ξi/||w|| = 0 である。このような総ペナルティを考えたときに、どのぐらいのペナルティならば許容できるのかを考える。例えば、誤分類サンプルをおおよそ K 個程度以下に抑えたいような場合は、上のペナルティに次のような制約条件を付ければよい。
\[ \sum_{i=1}^{n}\frac{\xi_{i}}{||\mathbf{w}||} \le K \]このとき、K を小さくすると、誤分類をほとんど許容しなくなるため、二つのクラスのサポート超平面間の距離が非常に短くなる。逆に K を大きくすると、誤分類を多く許容することになるので、二つのクラスのサポート超平面間の距離が非常に遠くなる。
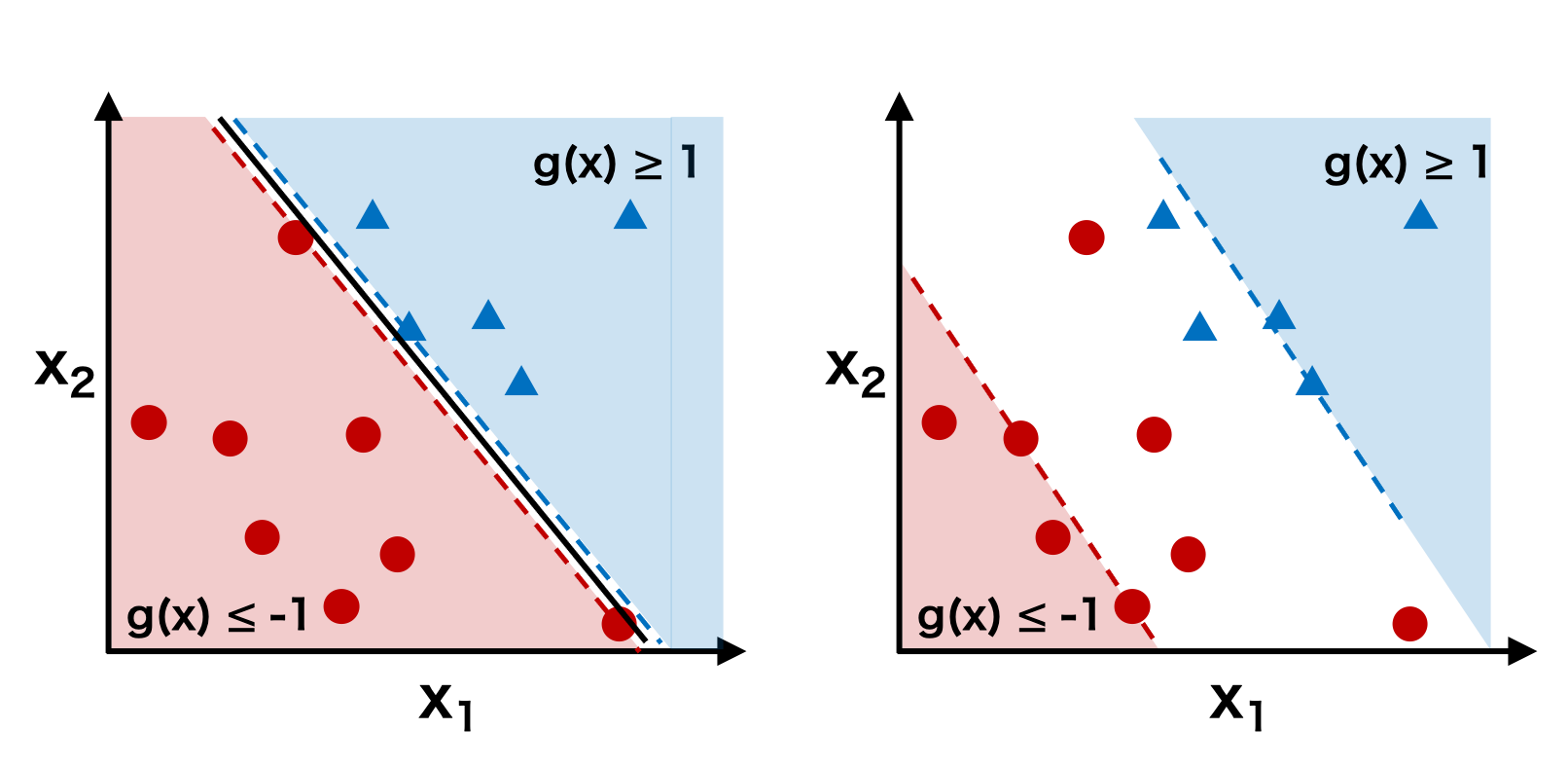
ソフトマージン法の定式化
以上のことから、SVM のソフトマージン法では、次のように定式化できる。
\[ \arg \max \left\{ \frac{2}{||\mathbf{w}||} \right\} \quad \text{subject to} \quad \sum_{i=1}^{n}\xi_{i} \le ||\mathbf{w}|| K \quad \xi_{i} \ge 0 \] \[ \quad (i = 1, 2, 3,\cdots) \]これをラグランジュの未定乗数法の式で書き直すと、次のようになる。
\[ \arg \max \left\{ \frac{2}{||\mathbf{w}||} \right\} + C\sum_{i=1}^{n}\xi_{i} \quad \xi_{i} \ge 0 \]C は定数で、誤分類を許容する指標 K と同じ役割を持つ。ソフトマージン法を利用するにあたり、C をあらかじめ与えておく必要があるので、C はハイパーパラメーターと呼ばれている。実際に、SVM を使って予測モデルを作成する上で、C は交差検証で最適な値に決められる。また、このハイパーパラメーター C にちなんで、ソフトマージン法は C-SVM などと呼ばれたりする。
パラメーター推定(最適化)
ラグランジュの未定乗数法によるパラメーター w の推定
ある関数を制約条件の元で最小化する方法としてラグランジュの未定乗数法がよく使われる。データ数が n 個あると、制約条件も n 個となるので、ここでラグランジュ未定乗数 αi および βi を n 個定義する。
\[ \boldsymbol{\alpha} = (\alpha_{1}, \alpha_{2}, \cdots, \alpha_{n}) \qquad \alpha_{i} \ge 0 \] \[ \boldsymbol{\beta} = (\beta_{1}, \beta_{2}, \cdots, \beta_{n}) \qquad \beta_{i} \ge 0 \]これを用いてラグランジュ関数 Lp を次のように定式化できる。
\[ L_{p} (\mathbf{w}, w_{0}, \xi, \alpha, \beta)= \frac{||\mathbf{w}||^{2}}{2} + C\sum_{i=1}^{n} \xi_i-\sum_{i=1}^{n}\alpha_i\bigl\{y^{(i)}(\mathbf{w}^T\mathbf{x}_i+b)-1+\xi_i\bigl\}-\sum_{i=1}^{n}\beta_i\xi_i \]このとき、||w||2/2 の最小化問題は次のように帰着できる。
\[ \arg \min_{\mathbf{w}} \left\{ L_{p} \right\} \quad \text{subject to} \quad \alpha_{i} \ge 0 \land \beta_{i} \ge 0 \quad (i = 1, 2, 3,\cdots, n) \]制約条件 (Ax ≥ b, x ≥ 0) のもとで ctx を最小化する問題は、双対定理に基づいて、制約条件 (Atx ≤ c, y ≥ 0) のもとで bty の最大化問題に置き換えて解くことができる。ここで、Lp の最小化問題の双対問題 LD に置き換えて、LD の最大化問題を解くことにする。
ここで、Lp に対して w、 w0 および ξ で偏微分して 0 とおくと、
\[ \frac{\partial L_{p} (\mathbf{w}, w_{0}, \xi, \alpha, \beta)}{\partial \mathbf{w}}= \mathbf{w} - \sum_{i=1}^{n}\alpha_iy^{(i)}\mathbf{x}_i=0 \] \[ \frac{\partial L_{p} (\mathbf{w}, w_{0}, \xi, \alpha, \beta)}{\partial w_{0}}= -\sum_{i=1}^{n}\alpha_iy^{(i)} = 0 \] \[ \frac{\partial L_{p} (\mathbf{w}, w_{0}, \xi, \alpha, \beta)}{\partial \xi} = C - \alpha_i - \beta_i = 0 \]これらの式を整理すると次のようになる。
\[ \mathbf{w} =\sum_{i=1}^{n} \alpha_i y^{(i)}\mathbf{x}_i \] \[ \sum_{i=1}^{n}\alpha_iy^{(i)} = 0 \] \[ C = \alpha_i + \beta_i \]偏微分で得られたこれらの式を、上のラグランジュ関数に代入すると、次のように α だけに関する式が得られる。これはハードマージン法と同じ形をした式である。
\[ L_{D}(\boldsymbol{\alpha}) = \sum_{i=1}^{n}\alpha_{i} - \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i}\alpha_{j}y^{(i)}y^{(j)}\mathbf{x}_{i}^{t}\mathbf{x}_{j} \]このとき、Lp の最小化問題は次のように LD の最大化問題に帰着できる。
\[ \arg \max_{\boldsymbol{\alpha}} \left\{ L_{D}(\boldsymbol{\alpha}) \right\} \quad \text{subject to} \quad \sum_{i=1}^{n}\alpha_{i}y_{i} = 0 \quad , \quad \alpha_{i} \ge 0 \]ラグランジュ未定乗数 α の推定
LD の最大化問題を解くアルゴリズムとして、逐次最小問題最適化法(sequential minimal optimization, SMO)が考案された。制約条件の下である変数 αi の値を変化させたとき、αi の変化分を吸収できるように他の変数 αj の値も変化させる必要がある。この考え方のもとで、変数の中からランダム αi と αj を選び両者の値を変化させるということを繰り返して、LD の最大値を逐次的に探索していく。
λ が求まれば、w を求めることができるようになりなる。
\[ \mathbf{w} = \sum_{i=1}^{n}\alpha_{i}y_{i}\mathbf{x}_{i} \]