ソフトマージン法の SVM では、線形分離不可能な問題に対して、分離境界線を超えて存在している点も許容することで、問題を解けるようにしてある。しかし、データの分布によっては、ソフトマージン法でも解けない問題がある。例えば、下図左に示してあるような 2 次元の特徴量を持ち、円状に分布しているデータの場合は、一つの分離超平面(直線)で 2 つのクラスを適切に分類することができない。このとき、2 次元の特徴量から新しい特徴量を作り出して、新しい特徴量を含めた多次元空間を使って SVM で分類を試みることができる。
下の図では、本来のデータには x1 および x2 という 2 つの特徴量しかない。この 2 つの特徴量では三角形と円形を分類できない。これに対して、この 2 つの特徴量から x12 + x22 を計算し、これを第 3 の特徴量として、データを 3 次元空間に配置すると、三角形と円形が適切に分類できるようになる。そこで、三角形と円形の間にある分離平面を SVM で求めれば、両者を分類できるようになる。言い換えれば、本来の特徴量をある関数 Φ に代入して、それを高次元空間に射影してから、SVM を適用するという作業を行っている。
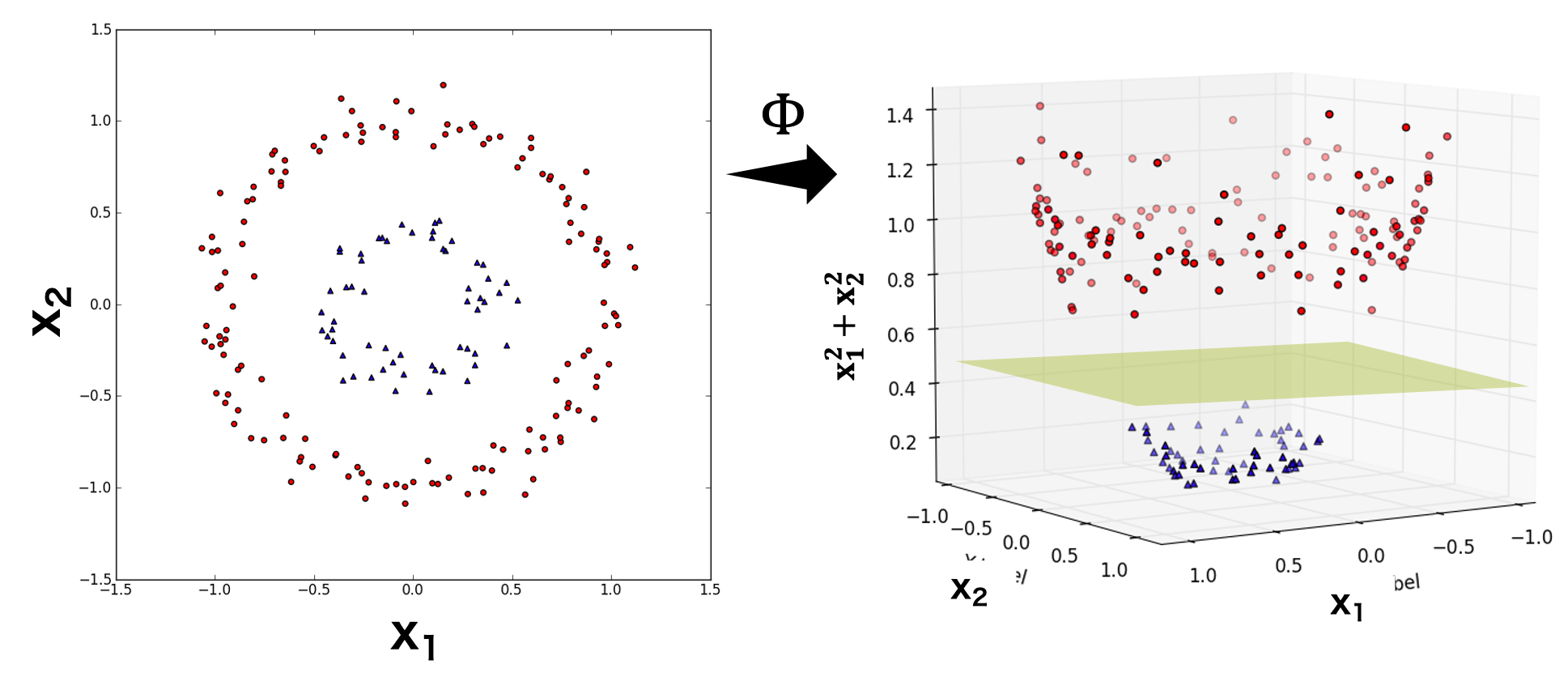
ここでは、2 次元の特徴量から 3 次元の特徴量を作成した。実際には、x1 および x2 から多数の特徴量を作り出すことができる。
\[ \begin{pmatrix} x_{1} & x_{2} & x_{1}^{2} & x_{2}^{2} & x_{1} + x_{2} & x_{1}x_{2} & x_{1}^{2} + x_{2}^{2} \end{pmatrix} \]高次元空間に射影された特徴量を z とする。高次元の特徴量 z に対して、SVM を適用するので、入力次元数は増えるものの、SVM のアルゴリズム自体は変わらない。その求め方は、本来の SVM の最適化式と同じものになる。しかし、特徴量の次元数が非常に大きい場合は、すべての特徴量 i および j に対して、zitzj を計算することになるため、計算量が膨大になる。
\[ L_{D}(\boldsymbol{\lambda}) = \sum_{i=1}^{n}\lambda_{i} - \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_{i}\lambda_{j}y_{i}y_{j}\mathbf{z}_{i}^{t}\mathbf{z}_{j} \]カーネルトリック
高次元の特徴量に対して zitzj を計算するには、膨大な計算量になる。zitzj は特徴量同士の内積を計算している。つまり、膨大な計算を行った後に得られる値が 1 つだけである。そこで、高次元の特緒量を利用した計算を避けながら、同じような効果が期待できるようなトリックについて考えてみる。
いま、本来のデータの特徴量 x = (x1, x2) を 2 次元の特徴量とする。2 次元の特徴量をある射影 Φ を行った結果、その特徴量が次のような 6 次元の特徴量 z になったとする。
\[ \mathbf{z} = \begin{pmatrix} 1 & \sqrt{2}x_{1} & \sqrt{2}x_{2} & \sqrt{2}x_{1}x_{2} & x_{1}^{2} & x_{2}^{2} \end{pmatrix} \]このとき、高次元において、特徴量 i および特徴量 j の内積 zitzj の計算式について式変更を行ってみる。
\[ \begin{eqnarray} && \mathbf{z}_{i}^{t}\mathbf{z}_{j} \\ &=& \begin{pmatrix} 1 & \sqrt{2}x_{i1} & \sqrt{2}x_{i2} & \sqrt{2}x_{i1}x_{i2} & x_{i1}^{2} & x_{i2}^{2} \end{pmatrix} \begin{pmatrix} 1 & \sqrt{2}x_{j1} & \sqrt{2}x_{j2} & \sqrt{2}x_{j1}x_{j2} & x_{j1}^{2} & x_{j2}^{2} \end{pmatrix} \\ &=& \left( 1 + 2x_{i1}x_{xj1} + 2x_{i2}x_{j2} + x_{i1}^{2}x_{j1}^{2} + 2x_{i1}x_{j1}x_{i2}x_{j2} \right)^{2} \\ &=& \left( 1 + x_{i1}x_{xj1} + x_{i2}x_{j2}\right)^{2} \\ &=& \left( 1 + \mathbf{x}_{i}\mathbf{x}_{j} \right)^{2} \end{eqnarray} \]すると、内積 zitzj を計算する代わりに、内積 xitxj を計算して定数項を足して 2 乗を行えば、同様な効果が得られることになる。このことから、Φ で射影するというトリックを行えば、射影先の高次元空間にある特徴量の形を自分で定義できないというデメリットがあるが、計算量が少なくて済むというメリットもある。
ここで低次元の特徴量を高次元の特徴量に射影する関数を、k(xi, xj) とおけば、関数 k は次のように書ける。
\[ k\left(\mathbf{x}_{i}, \mathbf{x}_{j} \right) = \left( 1 + \mathbf{x}_{i}\mathbf{x}_{j} \right)^{2} \]この関数 k にデータ本来の特徴量 xi および xj を代入することで、高次元への射影を行わなくても、高次元空間における内積を zitzj 計算できるようになる。このとき、SVM の最適化式中の内積 zitzj も高次元に射影することなく計算できるようになる。
\[ \begin{eqnarray} L_{D}(\boldsymbol{\lambda}) &=& \sum_{i=1}^{n}\lambda_{i} - \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_{i}\lambda_{j}y_{i}y_{j}\mathbf{z}_{i}^{t}\mathbf{z}_{j} \\ &=& \sum_{i=1}^{n}\lambda_{i} - \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_{i}\lambda_{j}y_{i}y_{j}\left( 1 + \mathbf{x}_{i}\mathbf{x}_{j} \right)^{2} \end{eqnarray} \]このように、本来は高次元空間で内積を計算しなければならないが、関数 k を使うことで、低次元空間での内積を計算しているのに、高次元空間で計算した内積と同じになるようなトリックをカーネルトリックとよぶ。このときに使った関数 k をカーネル関数とよぶ。
ここで使っているカーネル関数は、多項式カーネルと呼ばれるものである。このほかに、RBF カーネル、シグモイドカーネルなども考案されている。とりわけ、RBF カーネルがよく使われている。
カーネル関数
一般的に使われているカーネル関数には、次のような多項式カーネル、RBF カーネルおよびシグモイドカーネルなどがある。どのカーネル関数を選ぶかについては、基本的に交差検証を通じて決定してく。多くの場合、RBF カーネルが最も有効であることが多い。
多項式カーネル
多項式カーネルは、線形分離可能なデータには有効なカーネルである。ただ、そもそも線形分離可能ならば、線形 SVM を用いても解けるはずであるので、利用されるケースがあまりない。
\[ k\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) = \left(a + \mathbf{x}_{i}^{T}\mathbf{x}_{j}\right)^{b} \]RBF カーネル
線形分離不可能なデータに対して、RBF カーネルは非常に有効である。ただし、データが明らかに線形分離可能であることがわかれば、過学習にならないように線形 SVM や多項式カーネルを用いた方がよい。
\[ k\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) = \exp\left( - \frac{||\mathbf{x}_{i} – \mathbf{x}_{j} || ^{2}}{2\sigma^{2}} \right) \]シグモイドカーネル
シグモイドカーネルの計算は、入力特徴量に対して内積を計算し、それに重み a をかけてから定数項 b を足して、それを tanh 関数に代入して値を出力している。入力特徴量に対する計算 tanh(axitxj + b) は、ニューラルネットワークの中間層における計算と同等である。この中間層が出力した値が、SVM の分離超平面の計算に使われる。このように、シグモイドカーネルを使った SVM の一部は、ニューラルネットワークとほぼ同じしくみをしている。
\[ k\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) = \tanh \left( a\mathbf{x}_{i}^{T}\mathbf{x}_{j} + b \right) \]