サポートベクトルマシン(SVM)は、分類問題を解く機械学習アルゴリズムの一つである。SVM は、データを分類するための境界線(超平面)を求めることによって、予測モデルを構築している。超平面を求める方法として、ハードマージン法とソフトマージン法がある。ハードマージン法では、クラス間の距離(マージン)を最大となるように超平面を求めている。

ハードマージン法の定式化
パーセプトロンやロジスティック回帰においてデータを分類するとき、入力サンプル x に対して、重み w をかけてからバイアス w0 を足して得られる値が、正解ラベル y との誤差 ||wTx + w0 - y|| が最小となるように、重み w を推定している。SVM においても、同様な考え方が取り入れられている。ただし、正解ラベル y の値は、+1 または -1 としている。多クラス分類の場合は、C1 クラスとそれ以外、C2 クラスとそれ以外のような組み合わせで考える(One-vs-Rest)。
点と直線の距離
準備知識として、点と直線の距離を求める。ある直線 g(x) が係数(パラメーター)w0、w1、w2 を用いて、w0 + w1x1 + w2x2 = 0 とかけるものとする。ここで、ある点 P (p1, p2) から直線 g(x) 上に下ろした垂線の足を H (h1, h2) とする。このとき、線分 PH の長さは次のように求めることができる。
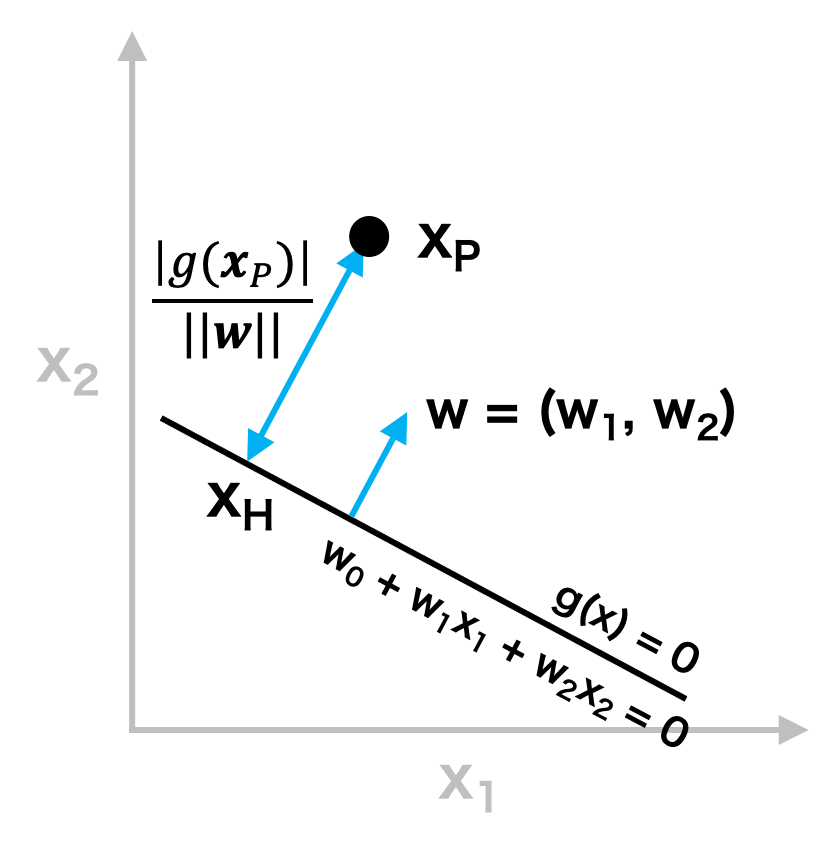
直線 g(x) の法線ベクトルを w とすると、w は、w = (w1, w2) とかける。このとき、\( \overrightarrow{PH} \) は法線ベクトル w に対して平行または逆平行であるので、ある実数 t が存在して、以下の関係が成り立つ。
\[ \overrightarrow{PH} = t \boldsymbol{w} \]ここで、両辺に w を書けて、式を展開すると
\[ \begin{eqnarray} \overrightarrow{PH} \cdot \boldsymbol{w} &=& t \boldsymbol{w} \cdot \boldsymbol{w} \\ (h_{1}-p_{1}, h_{2}-p_{2})\cdot(w_{1}, w_{2}) &=& t(w_{1}, w_{2})\cdot(w_{1}, w_{2}) \\ w_{1}(h_{1}-p_{1}) + w_{2}(h_{2}-p_{2}) &=& t(w_{1}^{2} + w_{2}^{2}) \end{eqnarray} \]\( w_{1}^{2} + w_{2}^{2} \ne 0 \) なので、両辺を \( w_{1}^{2} + w_{2}^{2} \) で割ると、
\[ t = \frac{w_{1}(h_{1}-p_{1}) + w_{2}(h_{2}-p_{2}) }{w_{1}^{2} + w_{2}^{2}} \]そこで、線分 PH の長さは、
\[ \begin{eqnarray} |\overrightarrow{PH}| &=& |t| |\boldsymbol{w}| \\ &=& \left | \frac{w_{1}(h_{1}-p_{1}) + w_{2}(h_{2}-p_{2}) }{w_{1}^{2} + w_{2}^{2}} \right |\sqrt{w_{1}^{2}+w_{2}^{2}} \\ &=& \frac{ | w_{1}h_{1} - w_{1}p_{1} + w_{2}h_{2} - w_{2}p_{2} | }{\sqrt{w_{1}^{2} + w_{2}^{2}}} \\ \end{eqnarray} \]ここで、点 H が直線 g(x) 上にあることから、w0 + w1h1 + w2h2 = 0 が成り立つので、上の式は次のように書き換えることができる。
\[ \begin{eqnarray} |\overrightarrow{PH}| &=& \frac{|w_{0} + w_{1}p_{1} + w_{2}p_{2} |}{\sqrt{w_{1}^{2} + w_{2}^{2}}} \\ &=& \frac{|g(\boldsymbol{p})|}{|| \boldsymbol{w} ||} \end{eqnarray} \]以上により、点 P = (p1, p2) から直線 g(x) に下ろした垂線の長さ、すなわち点 P と直線 g(x) の距離は、次のように定式化できる。
\[ \frac{|g(\boldsymbol{p})|}{|| \boldsymbol{w} ||} \]マージン最大化
ここで、例えば、下図のように、データが三角形または円形のいずれかに分類できるような 2 クラスの分類問題を考える。このとき、円形の点(negative data)に対して、
\[ w_{0} + \mathbf{w}^{t}\mathbf{x}_{negative} \le -1 \]三角形の点(positive data)に対して、
\[ w_{0} + \mathbf{w}^{t}\mathbf{x}_{positive} \ge 1 \]を満たすような関数 g(x) = w0 + wtx を考える。
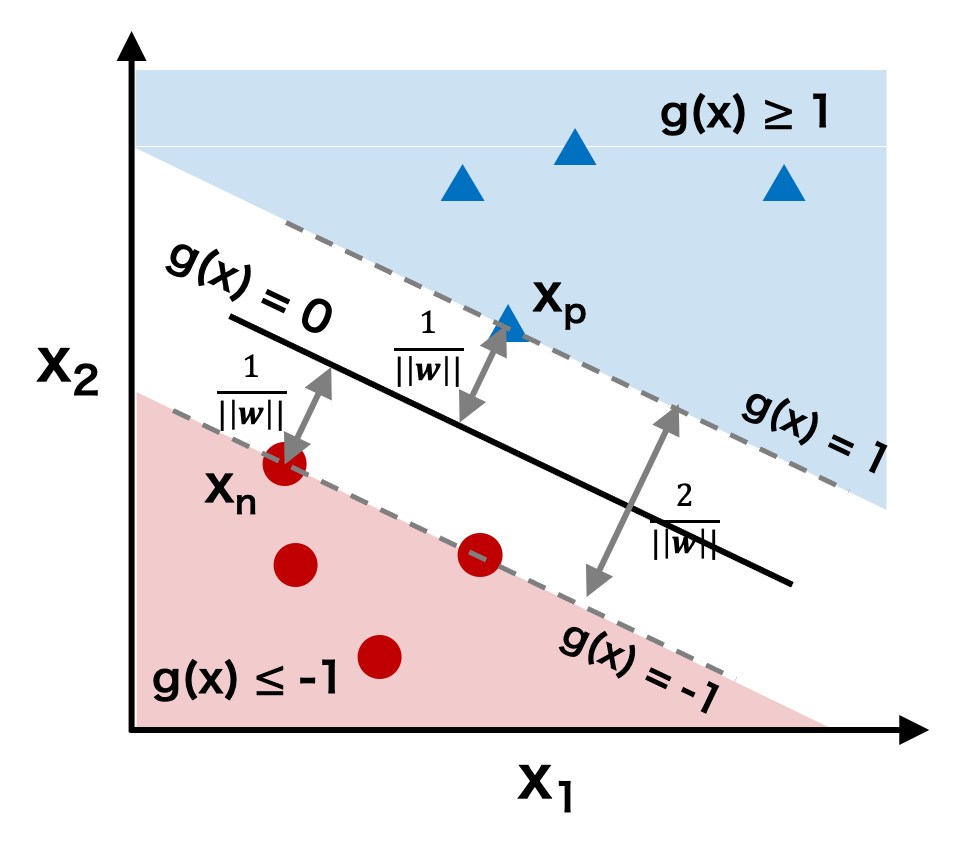
ここで、円形の点に着目すると、\( w_{0} + \mathbf{w}^{t}\mathbf{x} = -1 \) を満たす点 x = n が少なくとも 1 つ存在する。つまり、\( w_{0} + \mathbf{w}^{t}\mathbf{n} = -1 \) となる n が必ず存在する。その点 n から関数 g(x) までの距離を計算すると、点と距離の公式により、
\[ \frac{|g(\boldsymbol{n})|}{|| \boldsymbol{w} ||} = \frac{|w_{0} + \mathbf{w}^{t}\mathbf{n}|}{||\boldsymbol{w}||} = \frac{|-1|}{||\boldsymbol{w}||} = \frac{1}{||\boldsymbol{w}||} \]同様に、三角形の点に着目すると、\( w_{0} + \mathbf{w}^{t}\mathbf{p} = 1 \) を満たす点 p が少なくとも 1 つ存在する。その点 p から関数 g(x) までの距離も次のように計算できる。
\[ \frac{|g(\boldsymbol{p})|}{|| \boldsymbol{w} ||} = \frac{|w_{0} + \mathbf{w}^{t}\mathbf{p}|}{||\boldsymbol{w}||} = \frac{|1|}{||\boldsymbol{w}||} = \frac{1}{||\boldsymbol{w}||} \]円形の点は g(x) ≤ -1 であり、三角形の点は g(x) ≥ 1 であるから、両者は関数 g(x) によって分離されている。そして、円形形赤色領域と三角形青色領域の最短距離は、「円形の点 n から関数 g(x) までの距離」と「三角形の点 p から関数 g(x) までの距離」の和に等しい。すなわち、
\[ \frac{1}{||\boldsymbol{w}||} + \frac{1}{||\boldsymbol{w}||} = \frac{2}{||\boldsymbol{w}||} \]三角形の点と円形の点をもっともよく分類できるような関数 g(x) を求めるには、三角形の点と円形の点の距離が最も遠くなるようにすればよく、すなわち、2/||w|| を最大にすればよい。
\[ \arg \max_{\mathbf{w}} \left\{ \frac{2}{||\mathbf{w}||} \right\} \]2/||w|| を最大にすることは、||w||2/2 を最小にすることに等しい。よって上の式は次のように書き換えることができる。
\[ \arg \min_{\mathbf{w}} \left\{ \frac{||\mathbf{w}||^2}{2} \right\} \]制約条件
単に ||w||2/2 を最小にする w を求めるだけであれば、w = 0 とすればよいが、これでは初めの問題設定に反する。つまり、||w||2/2 を最小化を行うものの、最小化するときに、
\[ \begin{eqnarray} w_{0} + \mathbf{w}^{t}\mathbf{x}_{negative} &\le& -1 \\ w_{0} + \mathbf{w}^{t}\mathbf{x}_{positive} &\ge& 1 \end{eqnarray} \]という制約を満たさなければならない。
ここで、円形の点について y = -1、三角形の点について y = 1 とおいても一般性を失わない。このとき、ある点 i について、上の制約の式は y を用いて次のように 1 つの式で書き表わせる。
\[ y_{i}( w_{0} + \mathbf{w}^{t}\mathbf{x}_{i}) \ge 1 \]ハードマージン法の定式化
以上のことから、SVM のハードマージン法では、次のように定式化できる。ただし、図あるいは制約条件からもわかるように、マージンの最大化問題において、推定値が収束するのは、教師データがきれいに空間上で分離が可能な場合に限られる。
\[ \arg \min_{\mathbf{w}} \left\{ \frac{||\mathbf{w}||^{2}}{2} \right\} \quad \text{subject to} \quad y_{i}( w_{0} + \mathbf{w}^{t}\mathbf{x}_{i}) \ge 1 \quad (i = 1, 2, 3,\cdots)\]現実的に、分離しているデータが少ないと考えられるので、ハードマージン法が使われる機会が少ない。一般的に、データがきれいに分離していなくても使えるようなソフトマージン法がよく使われる。
パラメーター推定(最適化)
ラグランジュの未定乗数法によるパラメーター w の推定
ある関数を制約条件の元で最小化する方法としてラグランジュの未定乗数法がよく使われる。データ数が n 個あると、制約条件も n 個となるので、ここでラグランジュ未定乗数 λi を n 個定義する。
\[ \boldsymbol{\lambda} = (\lambda_{1}, \lambda_{2}, \cdots, \lambda_{n}) \] \[ \lambda_{i} \ge 0 \quad (i = 1, 2, 3, \cdots, n) \]これを用いてラグランジュ関数 Lp を次のように定式化できる。
\[ L_{p} (\boldsymbol{w}, w_{0}, \boldsymbol{\lambda}) = \frac{||\boldsymbol{w}||^{2}}{2} - \sum_{i=1}^{n}\lambda_{i}\left( y_{i}(w_{0} + \boldsymbol{w}^{t}\mathbf{x}_{i}) -1 \right) \]このとき、||w||2/2 の最小化問題は次のように帰着できる。
\[ \arg \min_{\mathbf{w}} \left\{ L_{p} \right\} \quad \text{subject to} \quad \lambda_{i} \ge 0 \quad (i = 1, 2, 3,\cdots, n) \]制約条件 (Ax ≥ b, x ≥ 0) のもとで ctx を最小化する問題は、双対定理に基づいて、制約条件 (Atx ≤ c, y ≥ 0) のもとで bty の最大化問題に置き換えて解くことができる。ここで、Lp の最小化問題の双対問題 LD に置き換えて、LD の最大化問題を解くことにする。
ここで、Lp に対して w および w0 で偏微分して 0 とおくと、
\[ \frac{\partial L_{p}}{\partial \mathbf{w}} = \mathbf{w} - \sum_{i=1}^{n}\lambda_{i}y_{i}\mathbf{x}_{i} = 0 \] \[ \frac{\partial L}{\partial w_{0}} = \sum_{i=1}^{n}\lambda_{i}y_{i} = 0 \]w および w0 の偏微分で得られた式を、上のラグランジュ関数に代入すると、次の式が得られる。
\[ L_{D}(\boldsymbol{\lambda}) = \sum_{i=1}^{n}\lambda_{i} - \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_{i}\lambda_{j}y_{i}y_{j}\mathbf{x}_{i}^{t}\mathbf{x}_{j} \]このとき、Lp の最小化問題は次のように LD の最大化問題に帰着できる。
\[ \arg \max_{\boldsymbol{\lambda}} \left\{ L_{D}(\boldsymbol{\lambda}) \right\} \quad \text{subject to} \quad \sum_{i=1}^{n}\lambda_{i}y_{i} = 0 \quad , \quad \lambda_{i} \ge 0 \]ラグランジュ未定乗数 λ の推定
LD の最大化問題を解くアルゴリズムとして、逐次最小問題最適化法(sequential minimal optimization, SMO)が考案された。制約条件の下である変数 λi の値を変化させたとき、λi の変化分を吸収できるように他の変数 λj の値も変化させる必要がある。この考え方のもとで、変数の中からランダム λi と λj を選び両者の値を変化させるということを繰り返して、LD の最大値を逐次的に探索していく。
λ が求まれば、w を求めることができるようになりなる。
\[ \mathbf{w} = \sum_{i=1}^{n}\lambda_{i}y_{i}\mathbf{x}_{i} \]