分類問題を解く機械学習アルゴリズム:サポートベクトルマシン
SVM
サポートベクトルマシン(Support Vector Machine; SVM)は分類問題を解く教師あり学習アルゴリズムの 1 つである。分類問題を解く機械学習アルゴリズムとして、ロジスティック回帰や決定木などがある。これらのアルゴリズムは、教師データをすべて使ってパラメーター推定を行い、予測モデルを構築している。これに対して、SVM では、分類に重要な一部の教師データ(サポートベクトル)のみを使ってモデルを構築している。さらに、SVM には、カーネルトリックとよばれる手法が取り入れられているため、線形分離不可能なデータにも対応できる。そのため、SVM は、ロジスティック回帰や決定木に比べて性能が高く、応用範囲が広いと言われている。
SVM はバイオインフォマティクスの分野でも積極的に使われている。例えば、一次構造であるアミノ酸配列から二次構造を予測したり、タンパク質がフォールディングする位置やタンパク質-タンパク質結合部位予測などで SVM が使われたりする。
サポートベクトルマシン
SVM では、教師データのうち、分類に重要な一部のデータだけを使って、予測モデルを構築している。C1 クラスと C2 クラスの 2 クラス分類問題を例にして考える。これらの教師データを多次元空間上にプロットすることで、C1 クラスの教師データと C2 クラスの教師データの境界線を調べることができる。
未知のデータを分類するにあたって、境界線の位置がわかれば、そのデータを分類できる。つまり、クラス同士の境界線を計算できれば予測モデルが作成される。この境界線を計算するにあたり、境界線近くにあるような教師データが重要で、境界線から遠く離れている教師データはそれほど重要でないと考えられる。SVM では、境界線近くにある一部の教師データを使って、境界線を表す関数を計算している。

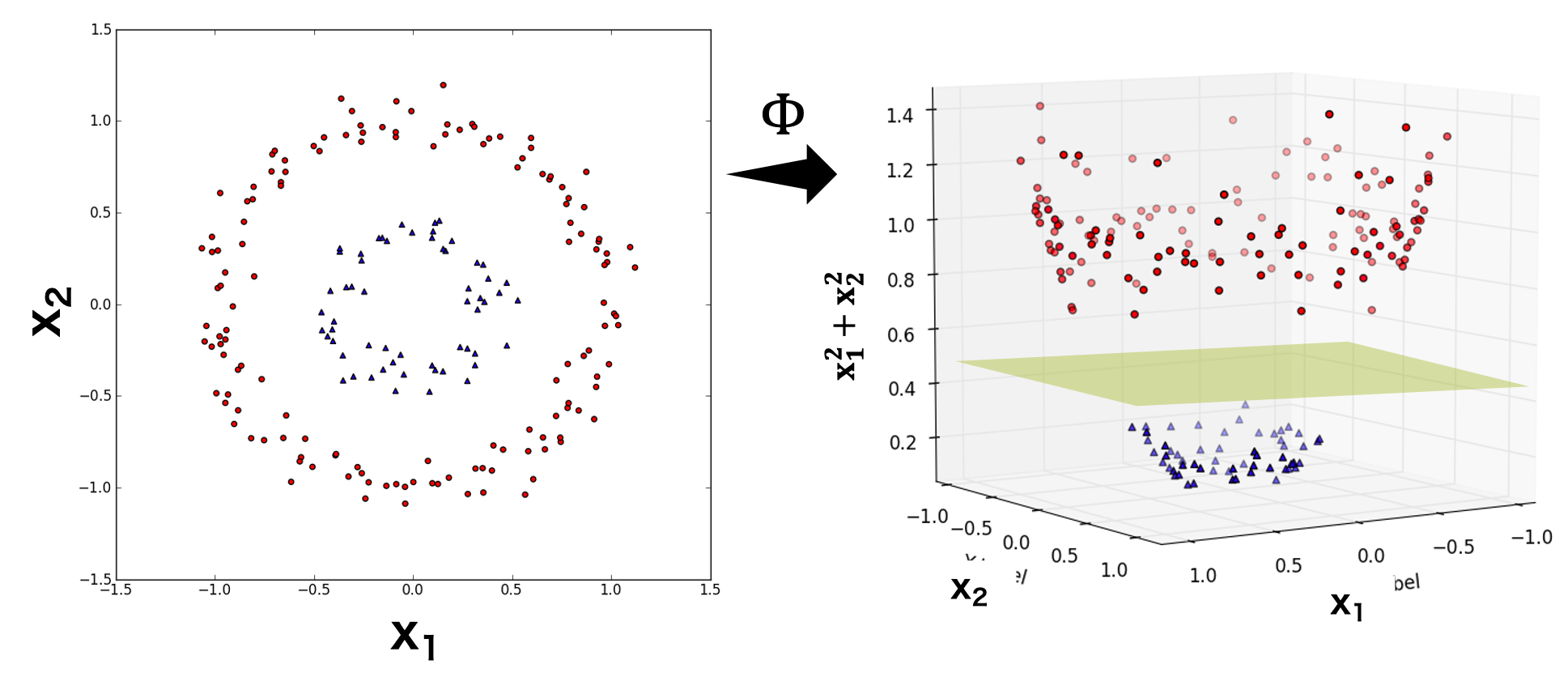
SVM では、境界線のことを超平面という。超平面を表す関数を分類関数という。分類関数を計算する方法にはハードマージン法とソフトマージン法がある。また、教師データの特徴量を機械的に増やして高次元データに変換した上で超平面を求めるカーネル法もある。