正則化は過学習を抑制するために使われる。予測モデルを構築するにあたり、モデルに組み込むパラメーター数(特徴量の数)を増減させることで、モデルの予測性能を変化させることができる。パラメーター数を増やせば、極端に言えば、パラメーター数を訓練サンプル数よりも多く設定することで、すべての訓練サンプルを正確に予測できるモデルが作られる。しかし、このように構築した予測モデルは訓練データに対して過学習を起こして、未知データに対しても同様な性能を発揮できると限らない。そのため、モデルを構築する際に、パラメーター数を増減させて、モデルの汎化性能をよくすることが求められる。
パラメーター数を解析者が増減させてモデルの訓練・評価を繰り返すこともできるが、予測アルゴリズムに組み込まれている手法を用いて自動的にパラメーター数を決めることもできる。その代表的な手法が正則化である。例えば、ロジスティック回帰には L1 および L2 正則化を設けることができるし、線形回帰分析にも L1 および L2 正則化を設けることができる。
正則化は次のように、損失関数に、λ||w||2 という罰則項を足すことによって設ける。λ を正則化パラメーターという。λ が大きくなれば、罰則項のウェイトが強くなり、||w||2 が小さくなる傾向が出てくる。つまり、w0, w1, w2, ... はゼロに近い値となったり、あるいはゼロとなったりするものが多くなる。
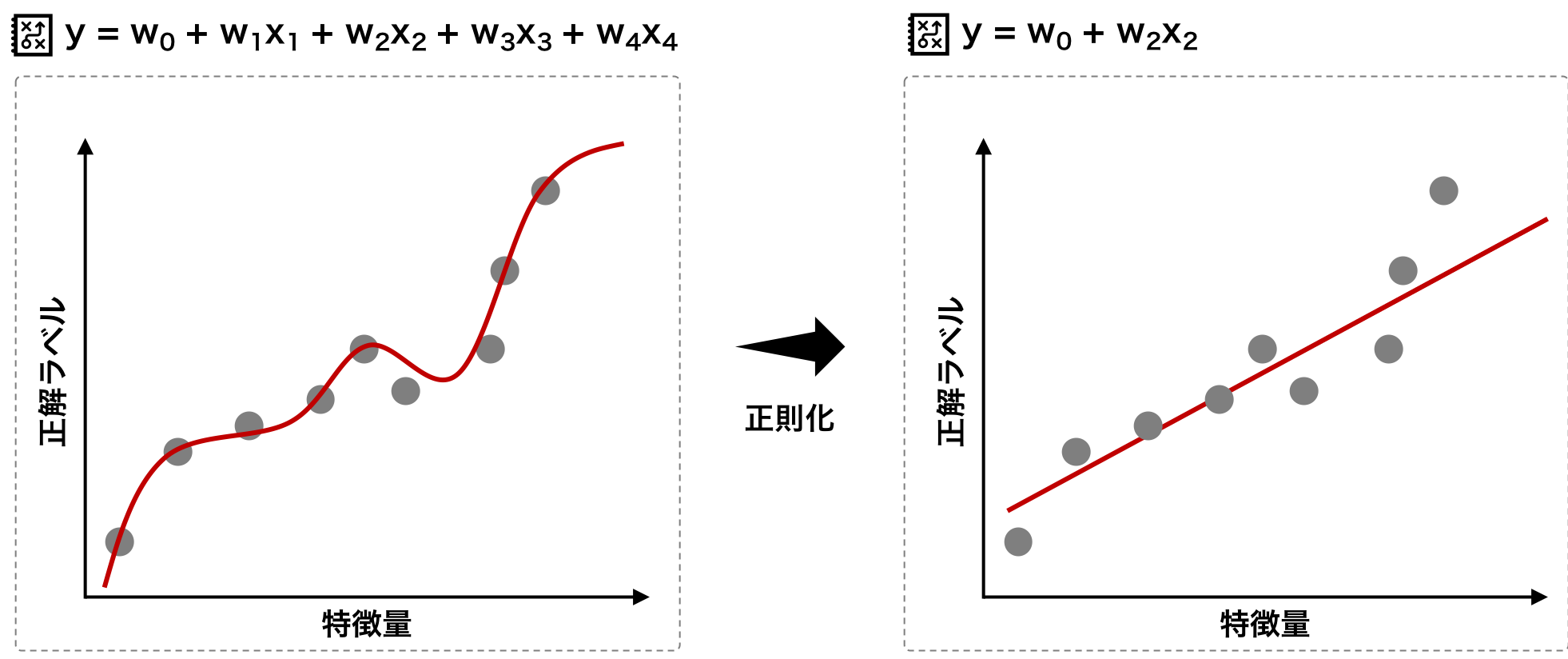
\[ loss(\mathbf{w}) = \parallel y-\mathbf{w}^{T}\mathbf{x} \parallel ^{2} + \lambda \parallel \mathbf{w} \parallel ^{2}\]図に示すと次のようになる。パラメーターの多いモデルでは、すべての学習データを正確に分類することができる。そこで、罰則項をもうけることで、(学習を通して、)いくつかの wi の値が 0 になり、モデルに含まれるパラメーターの数が減少する。