スケールの大きい特徴量では、0 付近の値でも 1000 付近の値でも同じ係数(パラメーター)がかかっている。このようなスケールの大きい特徴量の係数を推定するとき、値の大きなサンプルに影響されて、最適な係数を推定できなくなる。このようなスケールの大きいデータに対して、階級化、二値化、対数化などを行うことで、モデルの予測性能を向上させる場合が多い。
離散化
二値化
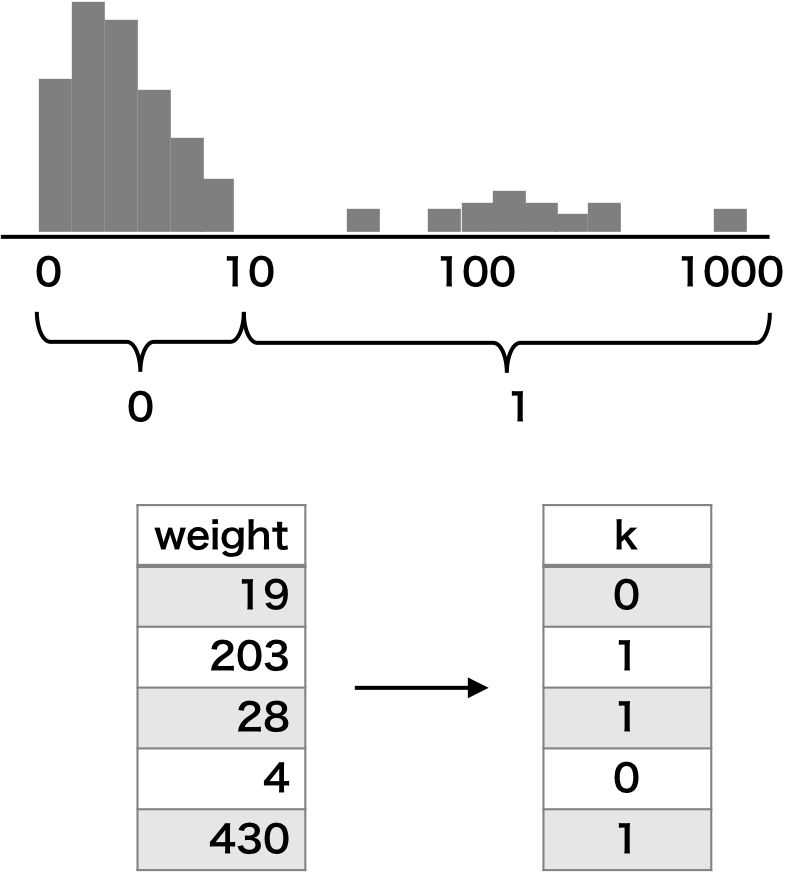
特徴量のスケールが大きく、その分布が広いとき、二値化を行うことで予測性能を向上させることがある。例えば、右の例ように、データの 90% が 10 以下の値を取り、残りの 10% が 10 よりも大きい値をとるような場合は、10 を閾値としてデータを 0 または 1 に変換すると、スケールの影響を大きく抑えることができるようになる。閾値の設定は、データの分布やドメイン知識などを考慮して決める。
階級化
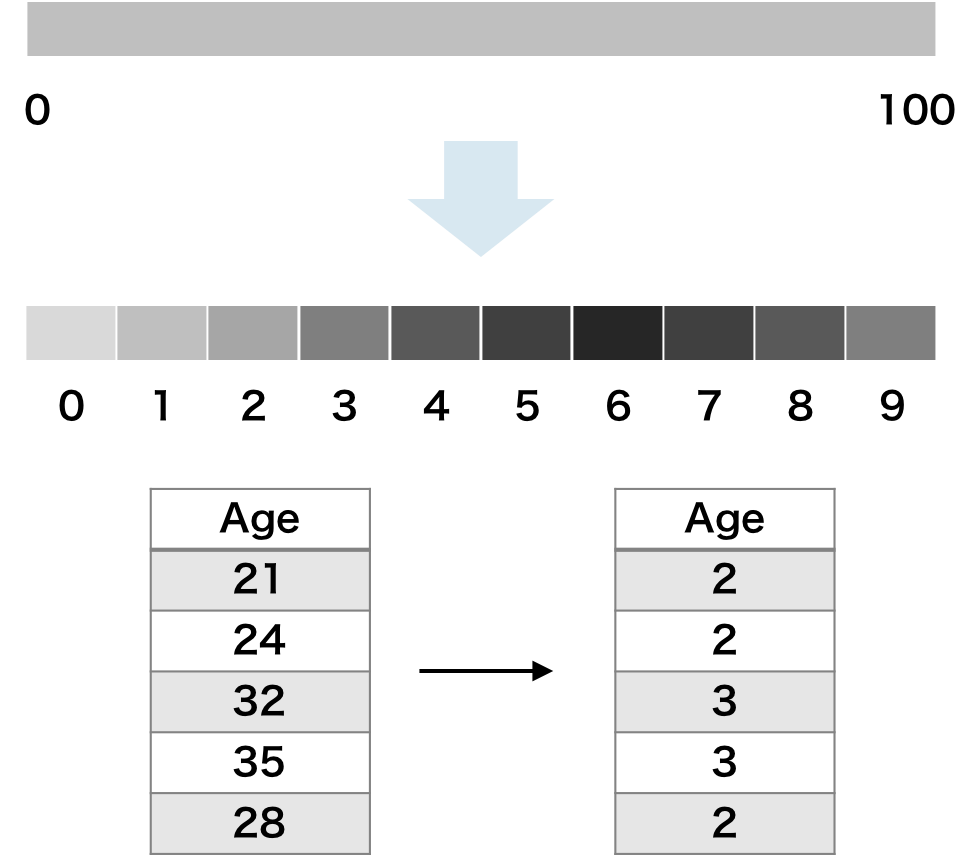
スケールの大きい特徴量を、いくつかの階級に分けることで、スケールを小さくすることができる。例えば、年齢データを 10 歳ごとに階級を決めて割り当てることで、0〜100 までのスケールをわずか 0〜9 までに縮小させることができる。
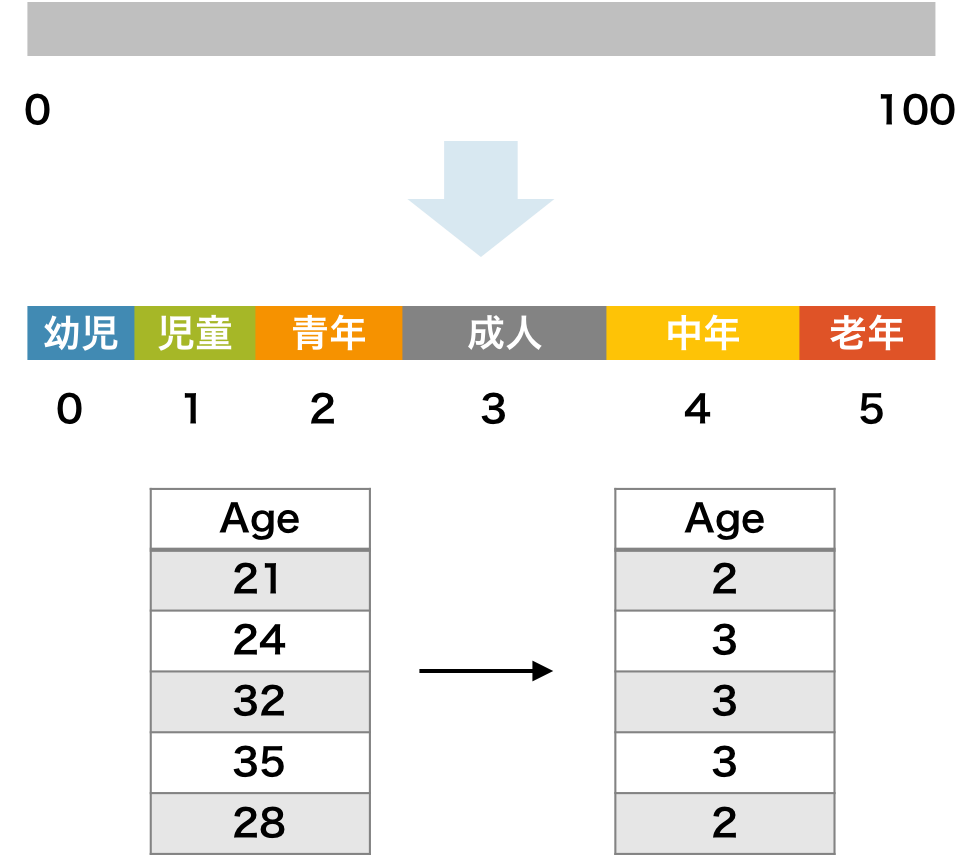
また、階級化は固定間隔で決める代わりに、ドメイン知識を使用して決めることもある。
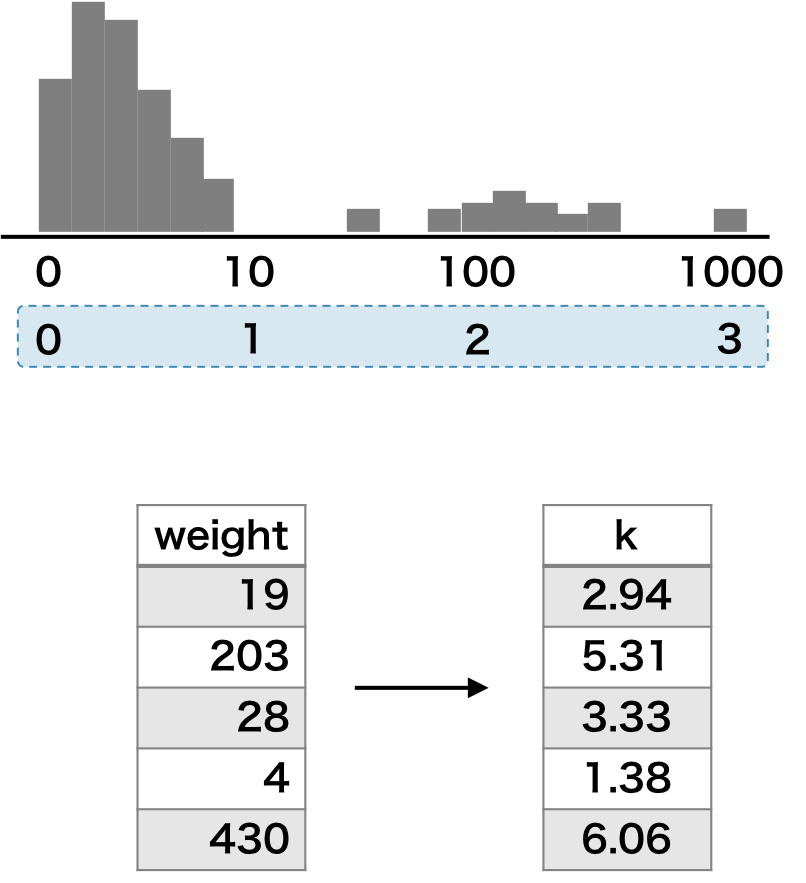
分位数
q-分位数を利用した離散化も取られている。例えば、四分位数を使用して、データ全体を 1, 2, 3, 4 の 4 つの階級に分けることができる。

累乗階級
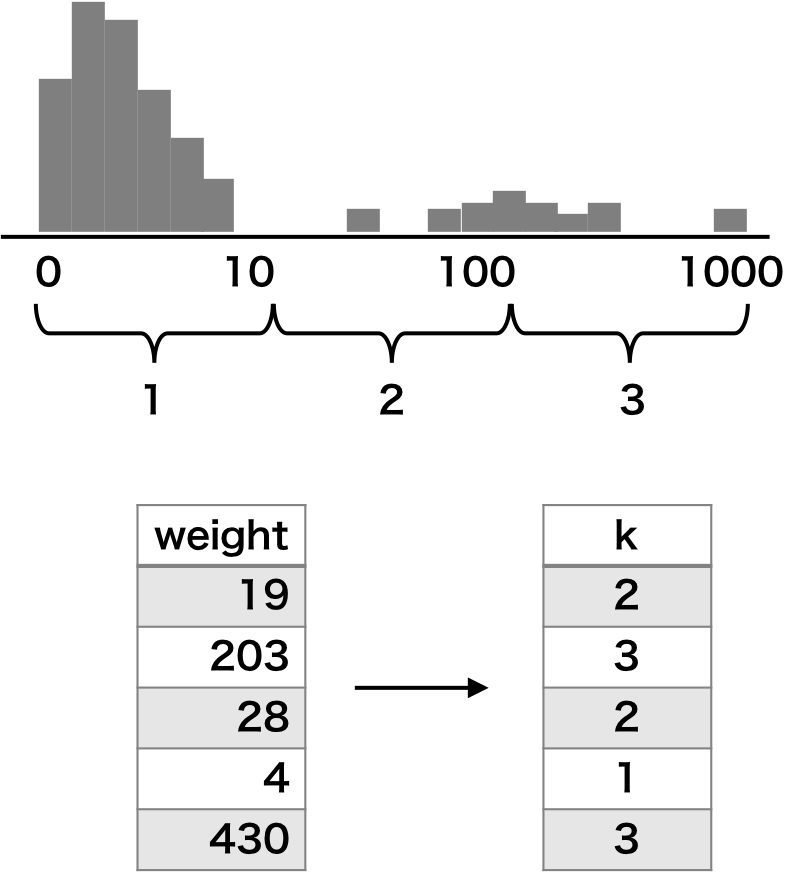
スケールの大きい特徴量に対して、10 の累乗で階級化することもある。
分散安定化変換
分散安定化変換は、分散が平均に依存しないように変数の分布を変換する操作である。その代表的な変換として Box-Cox 変換が一般的に知られている。対数変換や平方根変換なども Box-Cox 変換の特別な場合である。
対数化
スケールの大きい特徴量、とくに分布の裾の広い特徴量に対して、対数化することも、予測性能を上げるための有効な前処理法の一つである。対数化は、データに負の値が含まれると変換できないので、負の値が存在する場合は、定数を足してすべて正の値となるようにする。
Box-Cox 変換
Box-Cox 変換は次の式に基づいて変換が行われる。ハイパーパラメーター λ は、変換後のデータの分布が正規分布にもっとも近づくように決められる。
\[ \begin{eqnarray} z_{i} = \begin{cases} \frac{x^{\lambda}}{\lambda} & ( \lambda \ne 0 ) \\ \ln \lambda & ( \lambda = 0 ) \end{cases} \end{eqnarray} \]