主成分分析 PCA は、次元削減の目的で、統計学をはじめとする生物学やバイオインフォマティクスなど様々な分野で使われている。PCA は、機械学習の分野でも、多次元のデータを少次元のデータに縮約する目的で使われている。例えば、本来は p 個の特徴をすべて使ってデータを説明する必要がであるのに対して、PCA を利用して主成分を計算し、n (<< p) 個の主成分でデータの 90% を説明できるのならば、n 個の特徴を利用するよりも、より少ない m 個の主成分を解析に使った方が効率がよいと言える。次元削減することで、過学習を回避したり、計算コストを削減したりすることができる。とくに、p >> n の場合において、PCA による次元削減の効果が大きい。
主成分分析と固有値問題
主成分分析において主成分を求める問題は、行列の固有値問題に帰着できる。いま、行列 \(\mathbf{X}\) が n 個のサンプル、p 個の特徴量で構成されているとする。i 番目の特徴量を \(\mathbf{x}_{i} = (x_{1i}, x_{2i}, \cdots, x_{ni})^{T} \) で表し、全サンプルのデータからなる n × p の行列をベクトル表示で \(\mathbf{X} = (\mathbf{x}_{1}, \mathbf{x}_{2}, \cdots, \mathbf{x}_{n})\) と表す。
分散共分散行列
次に、p 個の特徴量のうち、k 番目と l 番目の特徴の共分散は、定義式に従って、次のように計算することができる。ここで、\( \mu_{k} = \sum_{j=1}^{n}x_{jk} \) とし、また、\( \mathbf{x'}_{k} = (x_{1k}-\mu_{k}, x_{2k}-\mu_{k}, \cdots, x_{nk}-\mu_{k})^{T} \) とした。
\[ \begin{eqnarray} Cov(\mathbf{x}_{k}, \mathbf{x}_{l}) &=& E\left[\left(\mathbf{x}_{k}-E[\mathbf{x}_{k}]\right)\left(\mathbf{x}_{l}-E[\mathbf{x}_{l}]\right)\right] \\ &=& \frac{1}{n}\sum_{j=1}^{n}\left( x_{jk} - \mu_{k} \right) \left( x_{jl} - \mu_{l} \right) \\ &=& \frac{1}{n}\mathbf{x'}_{k}^{T}\mathbf{x'}_{l} \end{eqnarray} \]p 個の特徴に対して、特徴のペア同士の共分散を、すべての組み合わせに対して計算すると、次のような分散共分散行列 Σ が得られる。ただし、\(\mathbf{X'} = (\mathbf{x'}_{1}, \mathbf{x'}_{2}, \cdots, \mathbf{x'}_{n} )\) とした。
\[ \mathbf{\Sigma}_{\mathbf{X}} = \begin{bmatrix} Cov(\mathbf{x}_{1}, \mathbf{x}_{1}) & Cov(\mathbf{x}_{1}, \mathbf{x}_{2}) & \cdots & Cov(\mathbf{x}_{1}, \mathbf{x}_{n}) \\ Cov(\mathbf{x}_{2}, \mathbf{x}_{1}) & Cov(\mathbf{x}_{2}, \mathbf{x}_{2}) & \cdots & Cov(\mathbf{x}_{2}, \mathbf{x}_{n}) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(\mathbf{x}_{n}, \mathbf{x}_{1}) & Cov(\mathbf{x}_{n}, \mathbf{x}_{2}) & \cdots & Cov(\mathbf{x}_{n}, \mathbf{x}_{n}) \end{bmatrix} = \frac{1}{n}\mathbf{X'}^{T}\mathbf{X'} \]
固有値問題
PCA の目標は、特徴量の分散が最大となるような次元を見つけることである。そのため、既存のデータ \(\mathbf{X}\) に対して座標変換を行い、変換後のデータの分散が最大となるような変換を見つければよい。ここで、\(\mathbf{X}\) に対して、座標変換を行うために、ある射影ベクトル \( \mathbf{w} \) をかけて、新しい座標を \(\mathbf{z}\) を計算する。このとき、n 次元であったサンプルの特徴量が射影ベクトル \( \mathbf{w} \) によって 1 つの点に置換されることに注意。
\[ \mathbf{z} = \mathbf{X}\mathbf{w} \]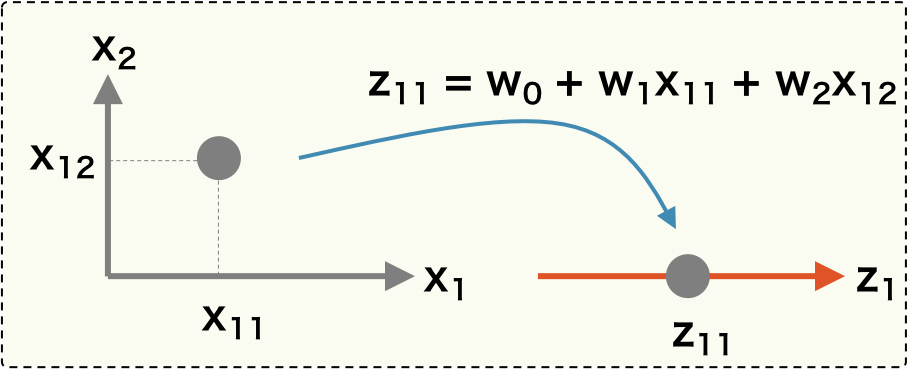
こうして得られた変換後の新しい座標 \(\mathbf{z} = (z_{1}, z_{2}, \cdots, z_{n})\) の分散を最大にするベクトル \(\mathbf{w}\) を求めればよい。そのために、\(\mathbf{z}\) の分散を計算する必要がある。上と同様にして、\(\mathbf{z}\) の分散は次のように計算できる。
\[ \mathbf{\Sigma}_{\mathbf{z}} = \frac{1}{n}\mathbf{z'}^{T}\mathbf{z'} \]\( \mathbf{z} = \mathbf{X}\mathbf{w} \) だから、\(\mathbf{z}\) の分散は、\(\mathbf{X}\) の分散共分散行列を使って次のように置き換えることができる。
\[ \begin{eqnarray} \mathbf{\Sigma}_{\mathbf{z}} = \frac{1}{n}\mathbf{z'}^{T}\mathbf{z'} &=& \frac{1}{n}(\mathbf{X'}\mathbf{w})^{T}(\mathbf{X'}\mathbf{w}) \\ &=& \frac{1}{n}\mathbf{w}^{T}\mathbf{X'}^{T}\mathbf{X'}\mathbf{w} \\ &=& \mathbf{w}^{T}\mathbf{\Sigma}_{\mathbf{X'}}\mathbf{w} \end{eqnarray} \]変換後のデータの分散を最大にしたいので、\(\mathbf{\Sigma}_{\mathbf{z}}\) となるようなベクトル \(\mathbf{w}\) を求めればよい。ベクトル \(\mathbf{w}\) は単位ベクトルなので、 \(||\mathbf{w}|| = 1\) という制約を利用すれば、ラグランジェの未定乗数法で \(\mathbf{w}\) を解くことができる。
\[ L(\mathbf{w}) = \mathbf{w}^{T}\mathbf{\Sigma}_{\mathbf{X}'}\mathbf{w} - \lambda (\mathbf{w}^{T}\mathbf{w} - 1) \]この式を最大化する \(\mathbf{w}\) は、関数 L を \(\mathbf{w}\) で偏微分した一次導関数を 0 と置くことで計算される。
\[ \frac{\partial L(\mathbf{w})}{\partial \mathbf{w}} = 2 \mathbf{\Sigma}_{\mathbf{X}'}\mathbf{w} - 2 \lambda \mathbf{w} = 0 \] \[ \mathbf{\Sigma}_{\mathbf{X'}}\mathbf{w} = \lambda\mathbf{w} \]このように PCA は固有値問題へと導かれる。データ \(\mathbf{X}\) が p 個の特徴量を持つとき、\( \Sigma_{\mathbf{X'}} \) は p×p の行列となるので、p 個の固有値が求まる。これら p 個の固有値を降順にならべて、λ1 > λ2 > λ3 > ... > λp とする。次に、それぞれの固有値 λi に対して固有ベクトル \(\mathbf{w}_{j}\) を求める。
主成分得点(主成分スコア)
p 個の固有値および固有ベクトルが求まると、行列 \(\mathbf{X}\) を回転させたあとの座標も計算できるようになる。例えば、k 番目の固有ベクトルを用いると、次のような回転後の座標が得られる。これを、第 k 主成分の主成分得点(主成分スコア)という。
\[ \mathbf{z}_{k} = \mathbf{X}\mathbf{w}_{k} \]主成分分析は、p 次元のデータを低次元に射影する次元削減に使われている。そのため、p 次元のデータを、第 1 主成分および第 2 主成分からなる二次元平面上にプロットしたり、あるいは第 3 主成分も含めて立体図にプロットしたりしてデータの分布状況を確認することが行われている。
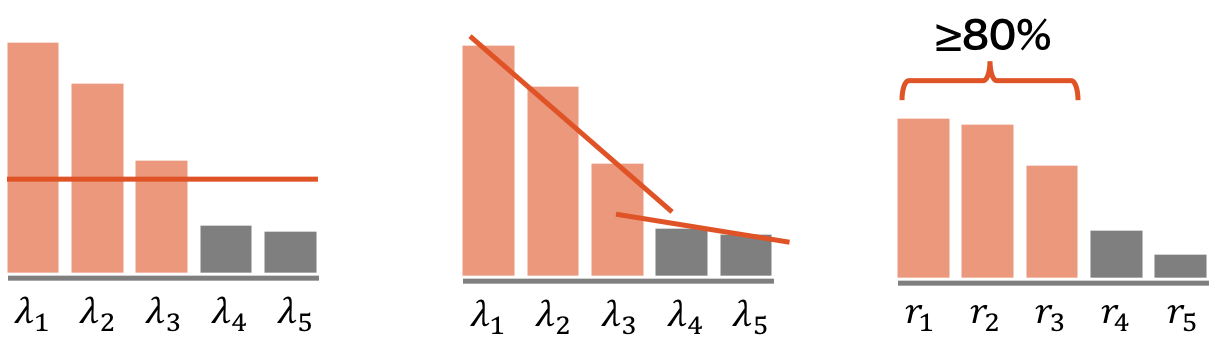
p 次元のデータを何次元に射影するか(主成分をいくつ選ぶか)は、研究分野や目的によって異なる。統計などであれば、例えば、ある閾値以上の分散(固有値)を持つ主成分を選ぶ、固有値の下がり具合が穏やかになったところまでの主成分を選ぶ、あるいは累積寄与率が 80-90% に達するまでの主成分を選ぶ、などの選び方がある。また、機械学習であれば、クロスバリデーションなどにより、最適な個数を見積もることもできる。
寄与率
第 k 主成分軸におけるデータの分散を計算すると、次のように λk として求まる。つまり、第 k 主成分軸におけるデータの分散は、k 番目に大きい固有値に等しい。
\[ \Sigma_{\mathbf{z}_{k}} = \mathbf{w}^{T}_{k}\Sigma_{\mathbf{X}}\mathbf{w}_{k} = \mathbf{w}^{T}_{k}\lambda_{k}\mathbf{w}_{k} = \lambda_{k}\mathbf{w}^{T}_{k}\mathbf{w}_{k}=\lambda_{k} \]各主成分の寄与率は、その主成分がデータが持つ全情報量のうち、どれぐらいの割合を説明できるのかを示している割合である。この寄与率は、次のように計算される。
\[ \frac{\lambda_{k}}{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{p}} \]また、第 1 主成分から第 k 主成分までの主成分を用いて説明できるデータの全情報量の割合を累積寄与率といい、次のように計算される。
\[ \frac{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{k}}{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{p}} \]主成分負荷量(因子負荷量)
観測データの各特徴量と各主成分の相関を主成分負荷量(因子負荷量)という。例えば、観測データの j 番目の特徴量と第 k 主成分の主成分負荷量は、次のようにして計算できる。bioplot をプロットしたとき、上で計算した相関係数を 10 倍した値が赤の矢印として描かれる。
\[ Cov(x^{'}_{j}, z^{'}_{k}) = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x}) (y_{i}-\bar{y})} {\sqrt{\frac{1}{n} \sum_{i=1}^{n}(x_{i}-\bar{x})^{2}} \sqrt{\frac{1}{n} \sum_{i=1}^{n}(y_{i}-\bar{y})^{2}}} \]PCA for MNIST data
MNIST は手書きの数字を画像にした画像データである。このデータセットには 28×28 ピクセルの画像が 7 万枚含まれている。実際の画像データは、1 枚につき 28×28 = 784 次元のベクトル mnist.data で構成されている。各画像には、その画像にどの数字(0〜9)が書かれているのかを示すラベル mnist.target がつけられている。
MNIST のデータセットをダウンロードするには、scikit-learn の featch_mldata メソッドを使用する。
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original', data_home='./data/minist')
print(mnist)
## {'DESCR': 'mldata.org dataset: mnist-original', 'COL_NAMES': ['label', 'data'], 'target': array([0., 0., 0., ..., 9., 9., 9.]), 'data': array([[0, 0, 0, ..., 0, 0, 0],
## [0, 0, 0, ..., 0, 0, 0],
## [0, 0, 0, ..., 0, 0, 0],
## ...,
## [0, 0, 0, ..., 0, 0, 0],
## [0, 0, 0, ..., 0, 0, 0],
## [0, 0, 0, ..., 0, 0, 0]], dtype=uint8)}
print(mnist.data.shape)
## (70000, 784)
print(mnist.target.shape)
## (70000,)PCA による次元削減
PCA を利用して画像の次元を削減する例を示す。ここでは、ダウンロードしてきた MNIST のデータに対して、標準化を行ってから、PCA による次元削減を行う。オリジナルの画像データの分散のうち 80% 以上説明できる主成分の数は、以下のように 150 個であることがわかる。つまり、オリジナルの画像データの分散を 100% 説明するには 784 個の変数(次元)を必要とするが、80% 説明するには 150 個の変数(主成分)だけで十分であるといえる。
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
img = mnist.data
# standardization & PCA
scaler = StandardScaler()
scaler.fit(img)
img_scaled = scaler.transform(img)
pca = PCA(0.80)
pca.fit(img_scaled)
print(pca.n_components_)
## 150
img_scaled_pca = pca.transform(img_scaled)次に、PCA による次元削減後の画像とオリジナルの画像を描き出して比べてみる。この際、次元削減した後のデータを元のデータと同じ次元数までに逆変換する必要がある。
import matplotlib.pyplot as plt
# get standardized & PCA-transformed data
img_lowdim = scaler.inverse_transform(pca.inverse_transform(img_scaled_pca))
plt.figure(figsize=(8,4))
# original image
plt.subplot(1, 2, 1)
plt.imshow(img[1].reshape(28,28),
cmap = plt.cm.gray, interpolation='nearest',
clim=(0, 255))
plt.title('original image', fontsize = 20)
# standardized & PCA-transformed image
plt.subplot(1, 2, 2)
plt.imshow(img_lowdim[1].reshape(28, 28),
cmap = plt.cm.gray, interpolation='nearest',
clim=(0, 255))
plt.title('80% of explained variance', fontsize = 20)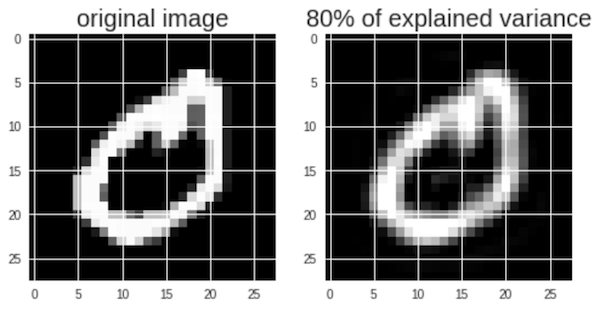
機械学習
MNIST データセットに対して標準化、PCA による次元削減を行ってからロジスティック回帰により機械学習モデルを作成する。MNIST データセットには 7 万枚の画像が含まれているが、このうち 8 割を学習データとしてモデルの学習に利用する。残りの 2 割のデータをテストデータとして、モデルの評価に利用する。
PCA for breast cancer data
次は、乳がんのデータに対して、PCA による次元削減を行なったあとに、ランダムフォレストによる予測モデルを行う例である。