線形判別分析(Linear Discriminant Analysis, LDA)は、特徴抽出の手法の一つで、次元削減の目的で使われる。主成分分析 PCA は、データの分散が最大となるような次元(軸)を探すのに対して、線形判別分析は、データのクラスを最もよく分けられる次元(軸)を探す。線形判別分析は、クラスの分け方が正確かどうかを判定するために、正解ラベルを必要とする。
線形判別分析
線形判別分析は、m 次元のデータ x を他の空間に写像し、写像後の空間においてデータを最も分類できるような写像を求める方法である。いま、仮に 2 次元の特徴量を持つデータが次のように分布しているものとする。
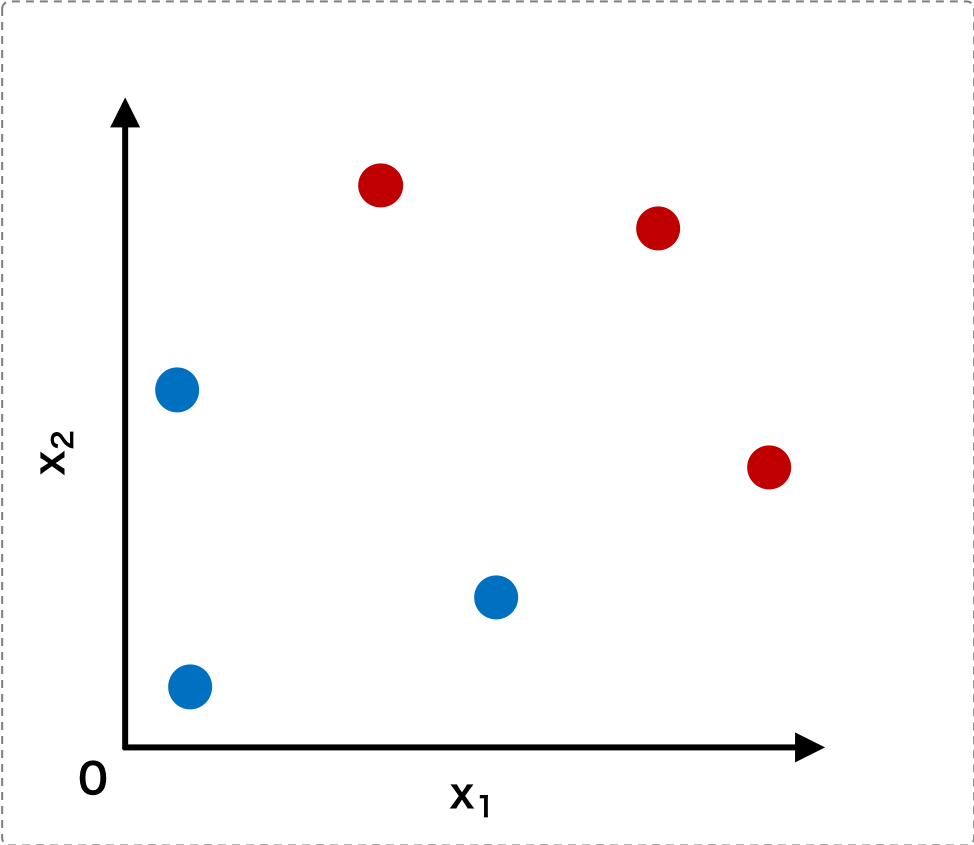
このデータをまず x1 軸上に写像すると、以下のようになる。この図から、x1 軸上に写像した場合、データをクラスごとに分離できないことがわかる。
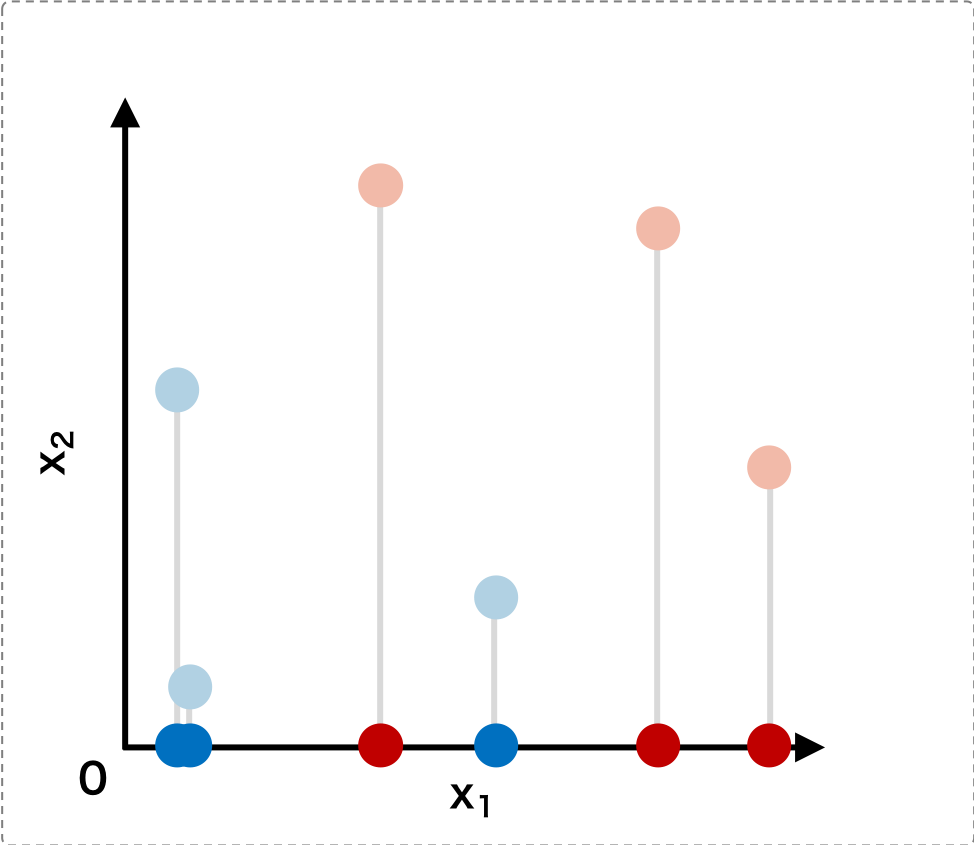
次に、このデータを x2 軸上に写像してみると、これも下の図から、データをクラスごとに分離できないことがわかる。
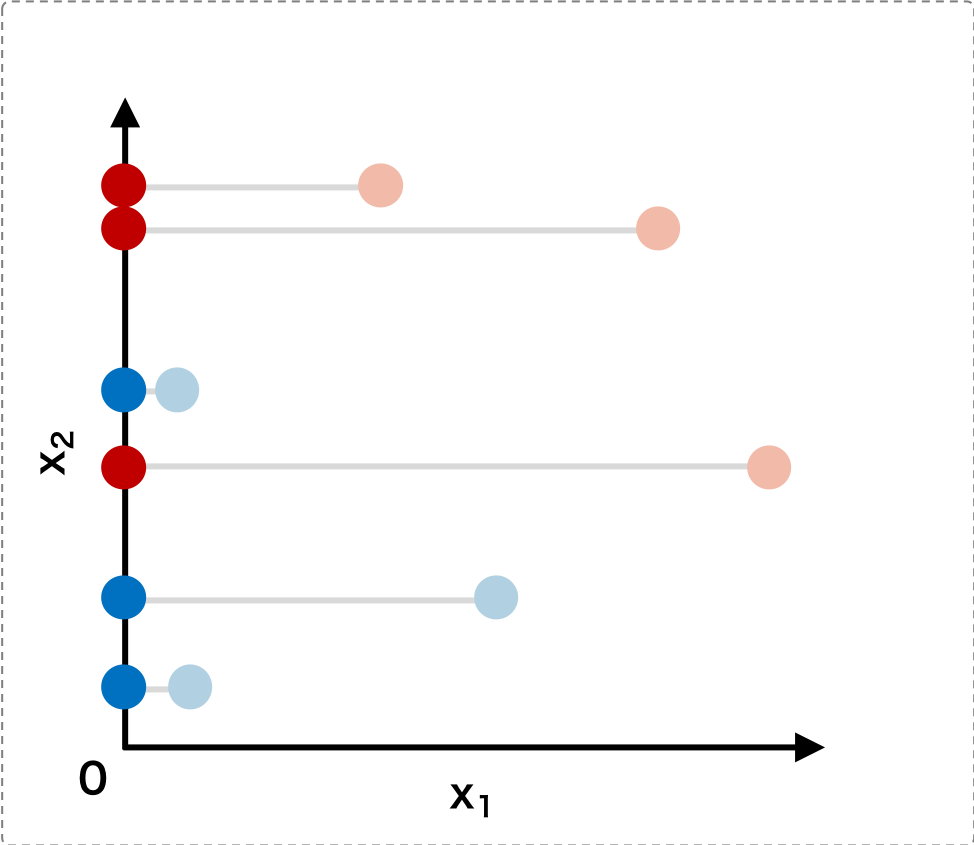
そこで、線形判別分析では、あるベクトル(回転行列) w を考えて、もとのデータ x にw をかけて、他の空間に線形写像し、その写像後の空間においてクラス分けが最もよくなるような w を求めることである
クラス平均間の距離
データをクラスごとに分離するための最適な射影を求めるためには、まず、射影後のクラス同士の分離の良さを測る指標を定義する必要がある。もっともシンプルな指標として、あるクラスの平均と他のクラスの平均との距離がある。例えば、2 クラス分類問題において、射影後のクラス 1 の平均 \(\boldsymbol{\mu}_{1} \) とクラス 2 の平均 \(\boldsymbol{\mu}_{2} \) の距離が大きく離れるほど、クラス 1 とクラス 2 の要素をうまく分類できたといえる。
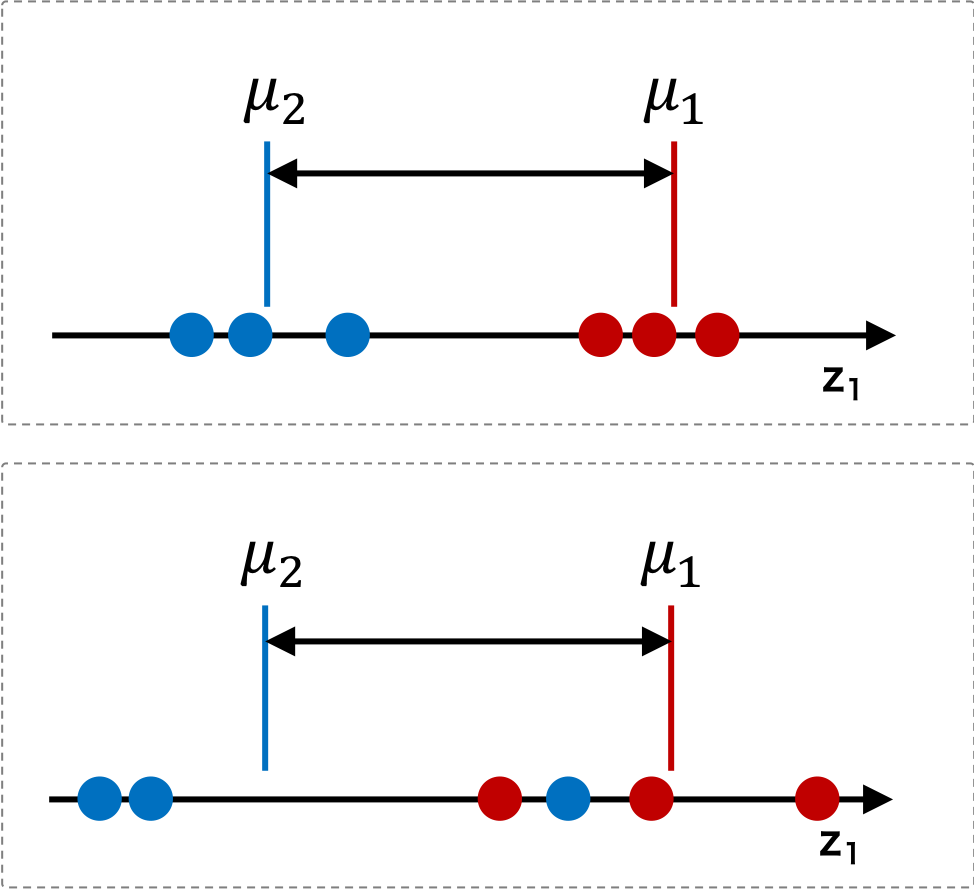
\[ J(\mathbf{w}) = | \boldsymbol{\mu}_{1} - \boldsymbol{\mu}_{2} |^{2} \]しかし、次の図に示したように、上のケースと下のケースとでは、クラス平均間の距離が等しい。それにもかかわらず、実際にデータをうまく分類できるのは、上のケースである。このことから、クラス平均の距離を分離の良さの指標として用いる場合は、不十分である。
クラス内分散
クラス平均の距離が長くなる以外に、クラス内の分散が小さくなる必要がある。言い換えると、データはクラスごとにまとまっていて、しかも、各塊の平均(重心)が互いに遠く離れているような状態が、もっとも分離が良いといえる。つまり、データをクラスごとに分離するための最適な射影を求めるためには、平均を考えるだけでは不十分であり、各クラス内の分散も同時に考える必要がある。
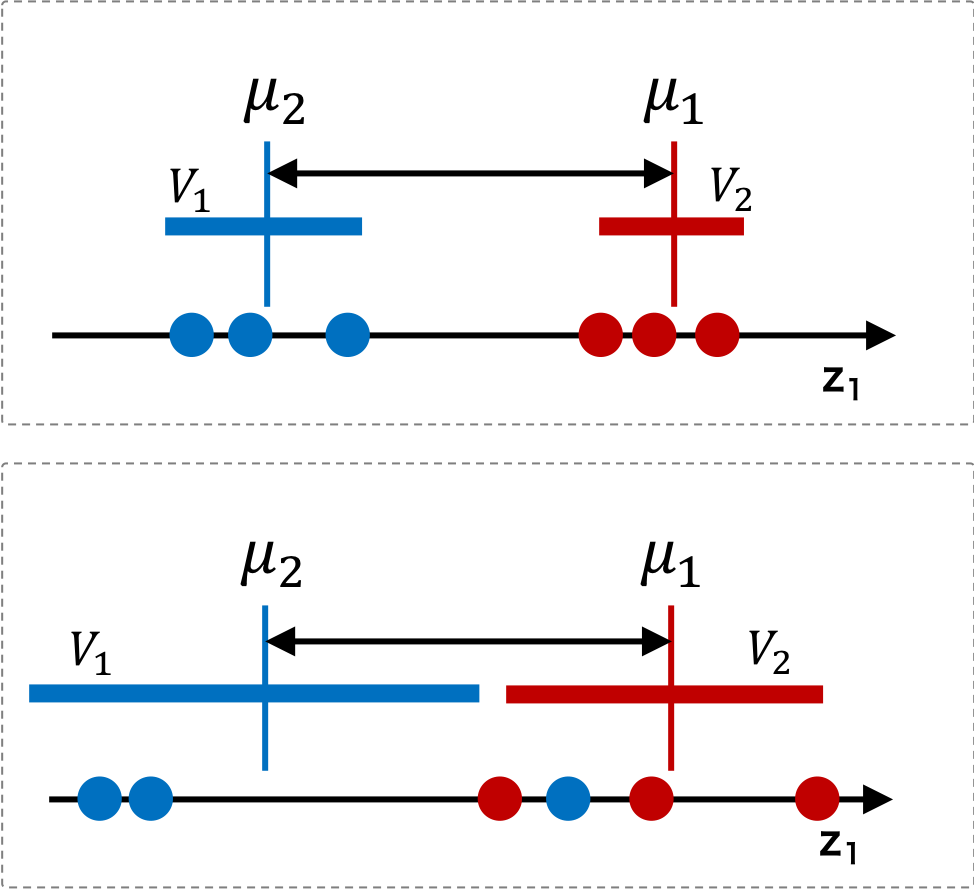
射影後のクラス 1 の分散を \( \mathbf{V}_{1} \) とし、クラス 2 の分散を \( \mathbf{V}_{2} \) としたとき、2 つのクラスがともにまとまっているときは、\( \mathbf{V}_{1} + \mathbf{V}_{2} \) が最小のときである。そこで、クラス平均間の距離とクラス内分散の両方の条件を満たすような評価関数を考えると、次のような関数が考えられる。
\[ J(\mathbf{w}) = \frac{|| \boldsymbol{\mu}_{1} - \boldsymbol{\mu}_2||^{2}}{\mathbf{V}_{1} + \mathbf{V}_{2}} \]評価関数
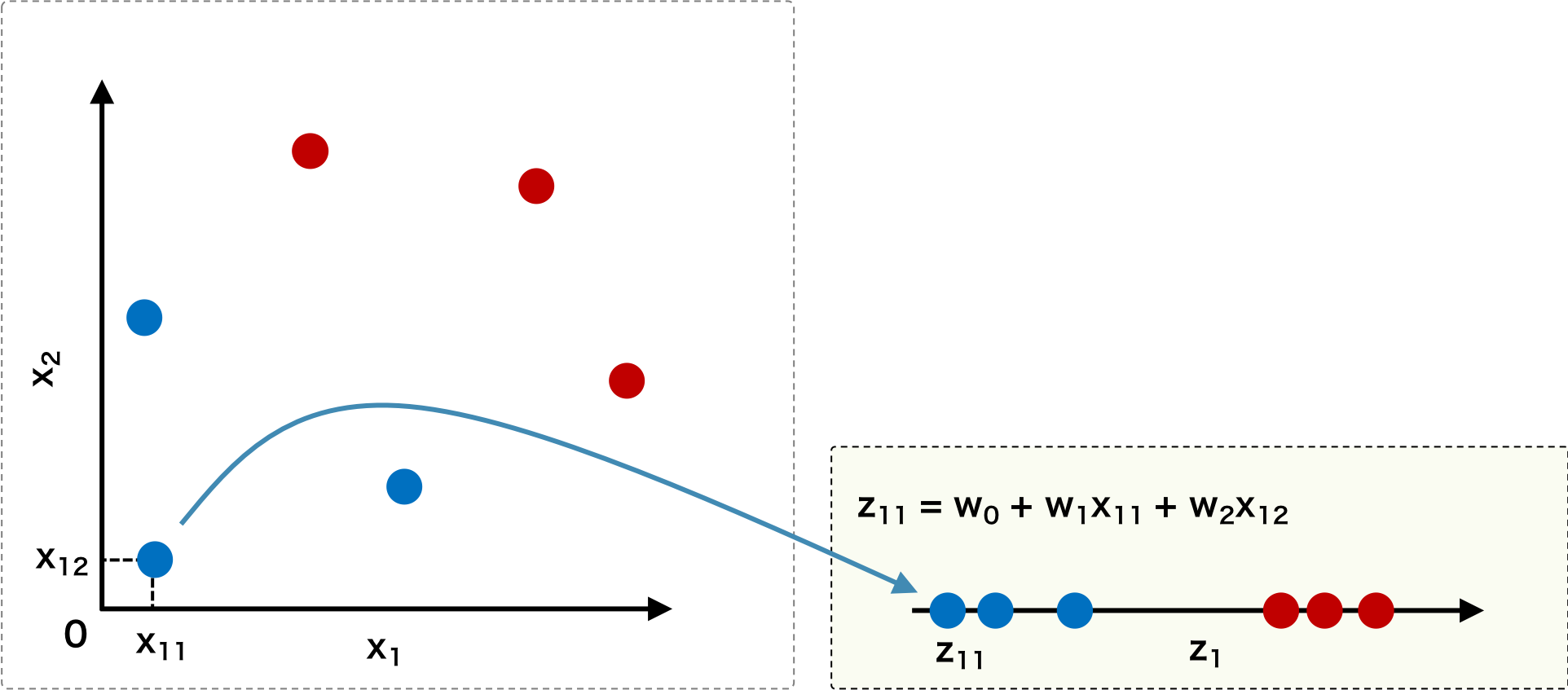
評価関数中の \( \boldsymbol{\mu}_{1} \) などは、射影後の空間の値を使用して表されている。これらを計算しやすいように、射影前の空間の値に変換しておく。そのためには、まず、射影後の空間におけるクラス c の平均と射影前の空間におけるクラス c の平均の関係を導く。ただし、射影後のデータの座標を y = wTx とする。
\[ \boldsymbol{\mu}_{c} = \sum_{\mathbf{x} \in c}\mathbf{y} = \sum_{\mathbf{x} \in c}\mathbf{w}^{T}\mathbf{x} = \mathbf{w}^{T}\sum_{\mathbf{x} \in c}\mathbf{x} = \mathbf{w}^{T}\boldsymbol{\mu}_{c} \]次に、射影後の空間におけるクラス c の分散と射影前の空間におけるクラス c の分散の関係を導く。
\[ \begin{eqnarray} \mathbf{V}_{c} = \sum_{\mathbf{x} \in c} \left( \mathbf{y} - \hat{\boldsymbol{\mu}}_{c} \right)^{2} &=& \sum_{\mathbf{x} \in c} \left( \mathbf{w}^{T}\mathbf{x} - \mathbf{w}^{T}\boldsymbol{\mu}_{c} \right)^{2} \\ &=& \sum_{\mathbf{x} \in c} \mathbf{w}^{T} \left(\mathbf{x} - \boldsymbol{\mu}_{c}\right) \left(\mathbf{x} - \boldsymbol{\mu}_{c}\right)^{T}\mathbf{w} \\ &=& \mathbf{w}^{T} \left( \sum_{\mathbf{x} \in c} \left(\mathbf{x} - \boldsymbol{\mu}_{c}\right) \left(\mathbf{x} - \boldsymbol{\mu}_{c}\right)^{T}\right)\mathbf{w} \\ &=& \mathbf{w}^{T}\Sigma_{X_{c}}\mathbf{w} \end{eqnarray} \]ここで、射影前と射影後の平均と分散の関係についても求められたので、評価関数の分子については、次のような書き換えを行うことができる。
\[ \begin{eqnarray} || \boldsymbol{\mu}_{1} - \boldsymbol{\mu}_{2} ||^{2} &=& \left(\mathbf{w}^{T}\overline{\mathbf{x}}_{1} - \mathbf{w}^{T}\overline{\mathbf{x}}_{2}\right)^{2} \\ &=& \mathbf{w}^{T}\left(\overline{\mathbf{x}}_{1} - \overline{\mathbf{x}}_{2}\right)\left(\overline{\mathbf{x}}_{1} - \overline{\mathbf{x}}_{2}\right)^{T}\mathbf{w} \\ &=& \mathbf{w}^{T}\mathbf{S}_{B}\mathbf{w} \end{eqnarray} \]次に、評価関数の分母については、次のような書き換えを行うことができる。
\[ \mathbf{V}_{1} + \mathbf{V}_{2} = \mathbf{w}^{T}\Sigma_{X_{1}}\mathbf{w} + \mathbf{w}^{T}\Sigma_{X_{2}}\mathbf{w} = \mathbf{w}^{T}(\Sigma_{X_{1}}+\Sigma_{X_{2}})\mathbf{w} = \mathbf{w}^{T}\mathbf{S}_{W}\mathbf{w} \]よって、評価関数は以下のように書き換えることができる。
\[ J(\mathbf{w}) = \frac{||\boldsymbol{\mu}_{1} - \boldsymbol{\mu}_2||^{2}}{\mathbf{V}_{1} + \mathbf{V}_{2}} = \frac{\mathbf{w}^{T}\mathbf{S}_{B}\mathbf{w}}{\mathbf{w}^{T}\mathbf{S}_{W}\mathbf{w} } \]この評価関数を最大化するような w を求めればよい。J(w) を最大化にする w が w' のとき、ある定数 k があり、kw' も J(w) を最大化にする。そこで、\( \mathbf{w}^{T}\mathbf{S}_{W}\mathbf{w} = 1\) という制約を設ける。
\[ \arg \max_{\mathbf{w}} \left\{ \mathbf{w}^{T}\mathbf{S}_{B}\mathbf{w} \right\} \quad \text{subject to} \quad \mathbf{w}^{T}\mathbf{S}_{W}\mathbf{w} = 1 \]ラグランジュの未定乗数法
これをラグランジュの未定乗数法により解いていく。
\[ L(\mathbf{w}) =\mathbf{w}^{T}\mathbf{S}_{B}\mathbf{w} - \lambda ( \mathbf{w}^{T}\mathbf{S}_{W}\mathbf{w} - 1 ) \]λ で偏微分して 0 とくことで、
\[ \mathbf{w}^{T}\mathbf{S}_{w}\mathbf{w} = 1 \]次に w で偏微分して 0 とおき、式を整理すると
\[ (\mathbf{S}_{B} - \lambda \mathbf{S}_{w})\mathbf{w} =\mathbf{0} \] \[ \mathbf{S}_{B}\mathbf{w} = \lambda \mathbf{S}_{w}\mathbf{w} \]この式の左から \(\mathbf{S}_{w}^{-1} \) をかけると、
\[ \mathbf{S}_{w}^{-1}\mathbf{S}_{B}\mathbf{w} = \mathbf{S}_{w}^{-1}\lambda \mathbf{S}_{w}\mathbf{w}=\lambda \mathbf{w} \]これにより、線形判別分析は固有値問題に帰着でき、固有値問題として解くことができる。
scikit-learn 実行例
次の例は、乳がんのデータセットを使用して、LDA による次元削減した後に、ランダムフォレストで予測モデルを作成する例である。この乳がんデータは 569 個のサンプル(診断ケース)を含む。1 つの診断に関して、腫瘍部分のサイズなどを含む 30 項目について調査が行われてた。このようなデータセットを使用して予測モデルを作成してみる。569 個のサンプルがあるので、8 割を学習に使用し、残りの 2 割をモデルの評価に使用する。学習は、入力データを標準化して、LDA により次元数を 2 次元までに削減した後に、ランダムフォレストにより予測モデルを作成する。