ホテリング理論は、データが正規分布に従うときに、外れ値（異常値）を検出する手法である。観測したデータ全体から平均値 μ および分散 σ² を計算します。観測データの中に異常値があるかどうかを調べる目的であれば、すべての観測データ x に対して、次式のように異常度 a(x) を計算する。新たに観測した未知のデータ x が外れ値かどうかを調べる目的であれば、未知のデータ x を次式に代入して異常度 a(x) を計算する。

x は正規分布に従うので、((x - μ) / σ) も正規分布に従う。そのため、その 2 乗値 ((x - μ) / σ)² は、（x が決まれば a(x) を計算できるので）、自由度 1 のカイ二乗分布に従う。そこで、このカイ二乗分布において、χ²(1; k) < α となる k を閾値とし、a(x) が k を超えているかどうかを調べて、外れ値判定を行う。

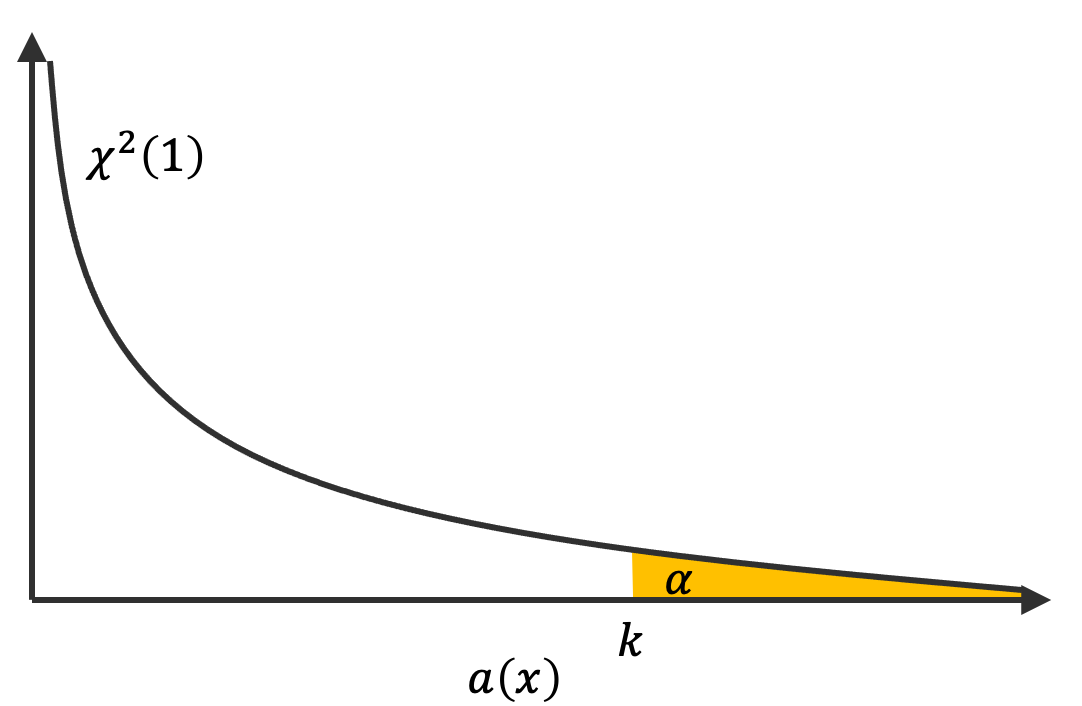
α （あるいは k）の設定については、目的に応じて決める。滅多に観測できないようなデータがきたとき、それを外れ値として検出したければ、例えば α = 0.01 のように決めることができる。この場合、「滅多に観測できない」というのは、μ および σ² の計算に使用したデータと同じ母集団から、新たに標本を抽出した場合、0.01 の確率でしか観測できないような極端に値の大きいまたは小さいデータのことを指す。

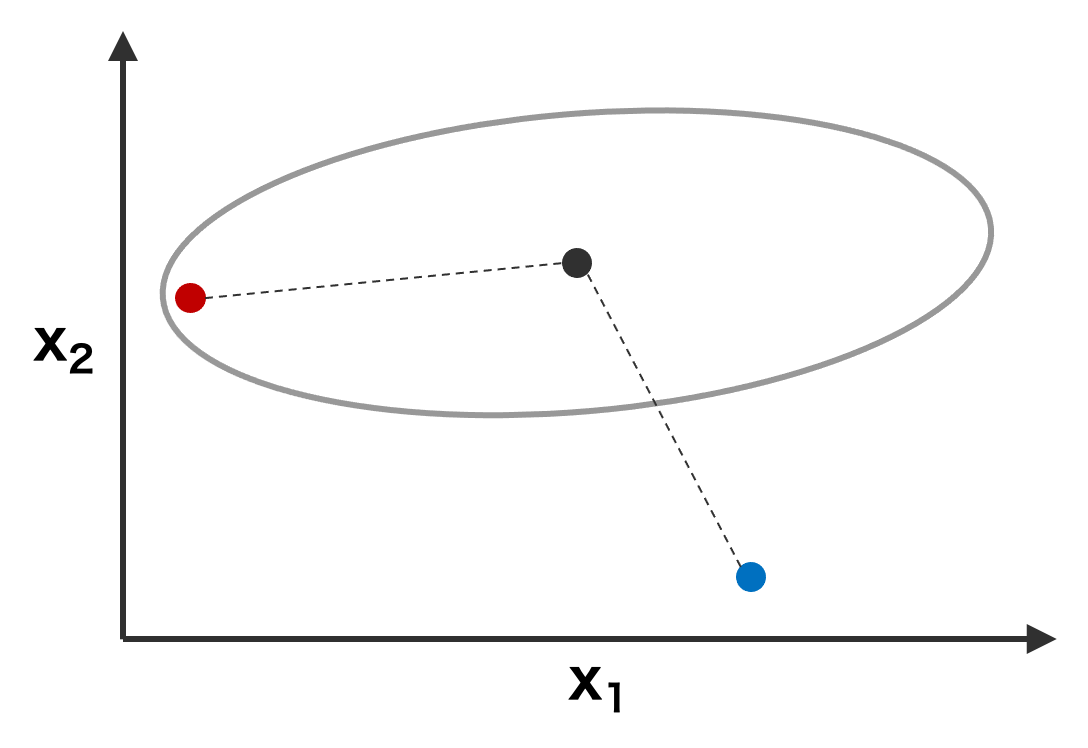
多次元のデータに対しては、マハラノビス距離を利用して異常度を計算する。特徴量が複数存在するとき、多次元空間上での特徴量は様々な方向に分布している。例えば、数のような二次元データの場合、特徴量 x₁ は広く分散しているのに対して、特徴量 x₂ はあまり分散していない。このような特徴量分布が存在したときに、ユークリッド距離を使って、分布の中心からどれぐらい離れているのかを異常度とすると、図中の赤点と青点は同じ異常度となる。しかし、特徴量の分布を考慮したとき、赤点が正常値で、青点が異常値であると考えた方が妥当で、両者の異常度が同じ値になるべきではない。そこで、多次元データの場合は、ユークリッド距離ではなく、データの分散も考慮したマハラノビス距離を使用した方が適切である。

ここで観測データの平均と分散共分散行列を次のように計算でき、

異常度は次のように計算できる。