Local outlier factor (LOF) は、あるサンプルの周辺に他のサンプルがどのぐらい分布しているのかという局所密度に着目して、外れ値の検出を行う方法である。ここで、ある点 P 局所密度について考える。点 P に最も近い k 個の近傍の点を Q1, Q2, ..., Qk とする。このとき、点 P の局所密度 ld(P) を次のように計算する。
\[ ld(P) = \frac{1}{k}\sum_{i=1}^{k}d(P, Q_{i}) \]次に点 P の周辺が点 Qi の周辺とどれぐらい異なっているのかについて計算する。両者の違いを比べるために、比 ld(Q)/ld(P) を利用する。点 Qi の周辺が密で、点 P の周辺が疎になっていれば、ld(Q)/ld(P) は大きな値をとる。また、点 Qi の周辺と点 P の周辺がほぼ同じぐらいの密度であれば、ld(Q)/ld(P) は 1 に近い値をとる。このようなことを点 P とすべての点 Qi (i = 1, 2, ..., k) について考えていったとき、点 P が、P 近傍にある k 個の点(Q1, Q2, ..., Qk)に比べて、どれぐらい異常なのかを計算できるようになる。そのような指標として、P と P 近傍の k 個の点との比 ld(Qi)/ld(P) の平均を用いることができる。
\[ lof(P) = \frac{1}{k}\sum_{i=1}^{k}\frac{ld(Q_{i})}{ld(P)} \]このように計算した lof(P) に対して閾値を設けて外れ値検知に利用する。
scikit-learn を使用する場合、LocalOutlierFactor 関数を利用する。このとき、未知の値に対してい外れ値検出を行いたい場合は、novelty=True を指定する必要がある。また、こうして作られたモデルに対して、訓練データを predict メソッドに代入して外れ値検知を行うと、間違った答えが帰ってくる。predict に代入できるのは、モデルの訓練に使用しなかったデータのみである。
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
print(__doc__)
np.random.seed(42)
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# training data
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# test data (normal)
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# test data (abnormal)
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
clf = LocalOutlierFactor(n_neighbors=20, novelty=True, contamination=0.1)
clf.fit(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure(figsize=(4, 4), dpi=150)
plt.title('Detection with LOF')
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')
s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s, edgecolors='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s,
edgecolors='k')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s,
edgecolors='k')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a.collections[0], b1, b2, c],
['learned frontier', 'training data',
'test data (normal)', 'test data (abnormal'],
loc="upper left",
prop=matplotlib.font_manager.FontProperties(size=11))
plt.show()学習データで決定された超平面は、次の図の赤色の曲線(輪)で囲まれている部分になる。
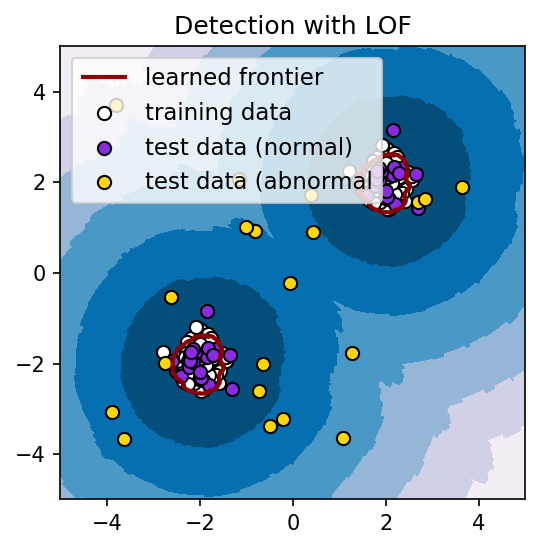
ハイパーパラメーターである contamination の値を変更することにより、外れ値の判定を強めたり、弱めたりすることができる。例えば、上記のコード中において、contamination = 0.0001 と値を小さくすると、分離超平面は次のようになる。
clf = svm.OneClassSVM(nu=0.2, kernel='rbf', gamma=0.1)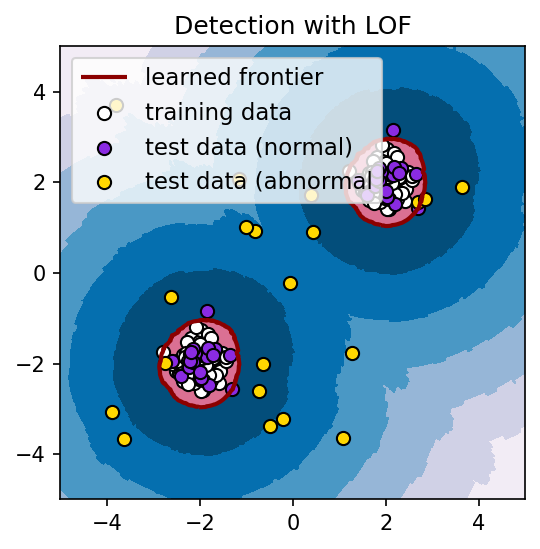
References
- Local Outlier Factor (LOF) による外れ値検知についてまとめた. hatenablog
- Novelty detection with Local Outlier Factor (LOF). scikit-learn