モデルの予測誤差は、ノイズ、バリアンス、およびバイアスに分解できる。ノイズは、データそのものに含まれているノイズであり、そのデータを使用すること以上、減らしたりすることができない。これに対して、バリアンスとバイアスは、予測モデルを作成する上で、モデルの複雑さを調整することで、減らしたり増やしたりすることができる。
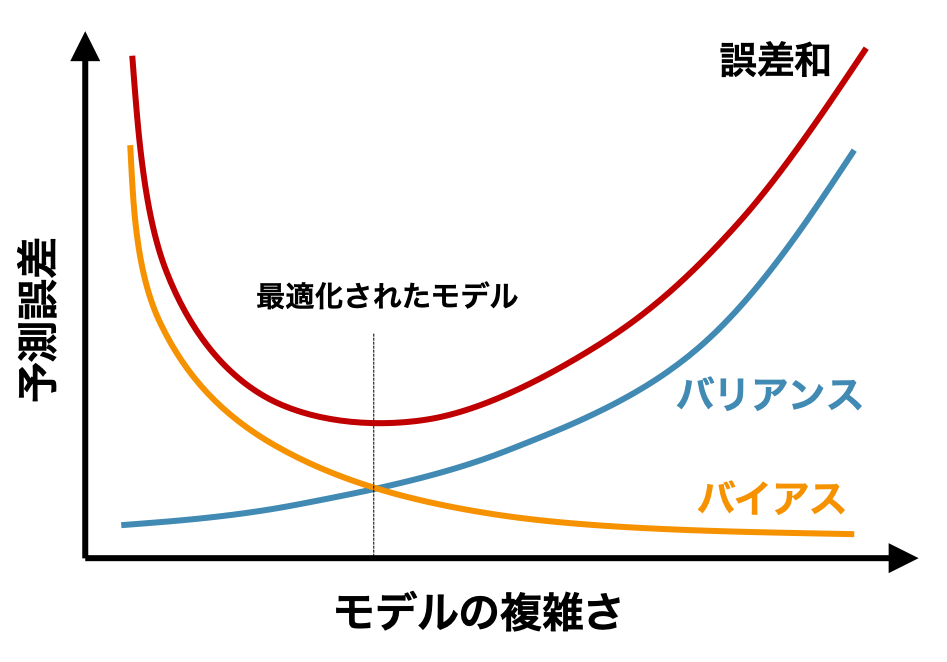
予測誤差の分解
ここで、予測誤差をノイズ、バリアンス、およびバイアスに分解する例を示す。二乗誤差をモデルの予測誤差の指標として考えた場合、真の値 y と予測された値 \(\hat{y}\) との間の二乗誤差は、次のようにかける。
\[ E\left[ (y - \hat{y})^{2} \right] \]この式を展開して、次のようにして、ノイズ項、バリアンス項、およびバイス項に分解することができる。ただし、期待値と分散の関係である Var[x] = E[x2] - (E[x])2 を使用した。
\[ \begin{eqnarray} E \left[ (y - \hat{y})^{2} \right] &=& E\left[ y^{2} + \hat{y})^{2} - 2y\hat{y} \right] \\ &=& E\left[ y^{2} \right] + E\left[ \hat{y}^{2} \right] -2E\left[ y\hat{y} \right] \\ &=& \left\{ Var[y] + (E[y])^{2} \right\} + \left\{ Var[\hat{y}] + (E[\hat{y}])^{2} \right\} + -2E\left[ y\hat{y} \right] \\ &=& Var[y] + Var[\hat{y}] + \left\{ (E[y])^{2} -2E\left[ y\hat{y}\right] + (E[\hat{y}])^{2} \right\} \\ &=& Var[y] + Var[\hat{y}] + \left\{ (E[y])^{2} -2E\left[ y \right] E \left[\hat{y}\right] + (E[\hat{y}])^{2} \right\} \\ &=& Var[y] + Var[\hat{y}] + \left( (E[y]) - (E[\hat{y}]) \right) ^{2} \\ &=& noise + variance + bias^{2} \end{eqnarray} \]ノイズ Var[y] は、データそのものに由来する分散であり、そのデータを使う限り避けてはならないものである。バリアンス \(Var(\hat{y})\) は、予測結果の分散である。そして、バイアスは、真の値と予測値の差である。この 3 つの項のうち、ノイズそのデータを使う限り定数となる。しかし、バリアンスとバイアスは、モデルの複雑さによって変化する。この際、バリアンスを小さくするとバイアスが大きくなり、バイアスを小さくするとバリアンスが大きくなるというトレードオフの関係が見られる。
バリアンスを小さくする
バリアンス \(Var[\hat{y}]\) を小さくするために、モデルの予測値をなるべく同じ値になるようにすればよい。そうすれば、\(Var[\hat{y}]\) の値が小さくなる。極端な例を上げると、すべてのパラーメーターをなくして、y = 1.0 となるような非常に単純なモデルを考えた場合、このモデルは、入力 x に関わらず、1.0 と予測する。このとき、バリアンス \(Var[\hat{y}]\) はゼロになる。しかし、このとき、真の値と予測値のズレが大きくなり、バイアス \( \left( (E[y]) - (E[\hat{y}]) \right) ^{2} \) が高くなる。
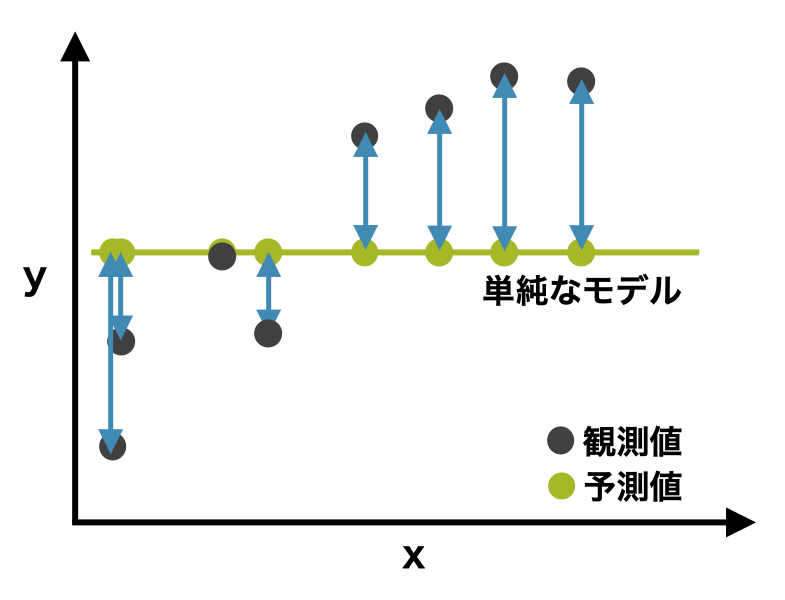
バイアスを小さくする
バイアスを小さくしたとき、逆にバリアンスが増える。極端な例をあげれば、非常に複雑なモデルを考えて、すべて訓練データを正確に予測する完璧なモデルを考える。このとき、バイアス \( \left( (E[y]) - (E[\hat{y}]) \right) ^{2} \) はゼロになる。しかし、予測値が上下に大きくブレるため、バリアンス \(Var[\hat{y}]\) が大きくなりがちになる。
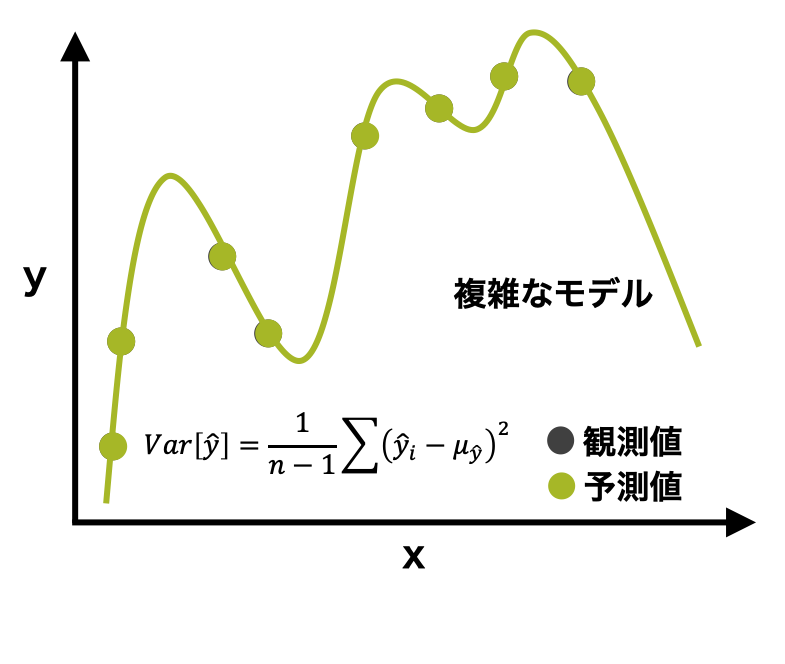
理想的には、バリアンスとバイアスの両方を最小化することが望ましいが、実際にはバリアンスとバイアスがトレードオフの関係にある。バリアンスを小さくするとバイアスが大きくなり、逆にバイアスを小さくするとバリアンスが大きくなる。