ロジスティック回帰は、二値分類を行うための分類モデルである。機械学習の予測モデルは、一般的に、特徴量ベクトル x とウェイト w の内積を計算し、その内積 z = wTx を活性化関数 f に代入し、その出力値 f(z) が閾値 θ 以上ならば 1、そうでなければ 0 を出力する。この 1 または 0 をもって二値分類を行う。ロジスティック回帰は、活性化関数 f をロジスティックシグモイド関数とした場合である。
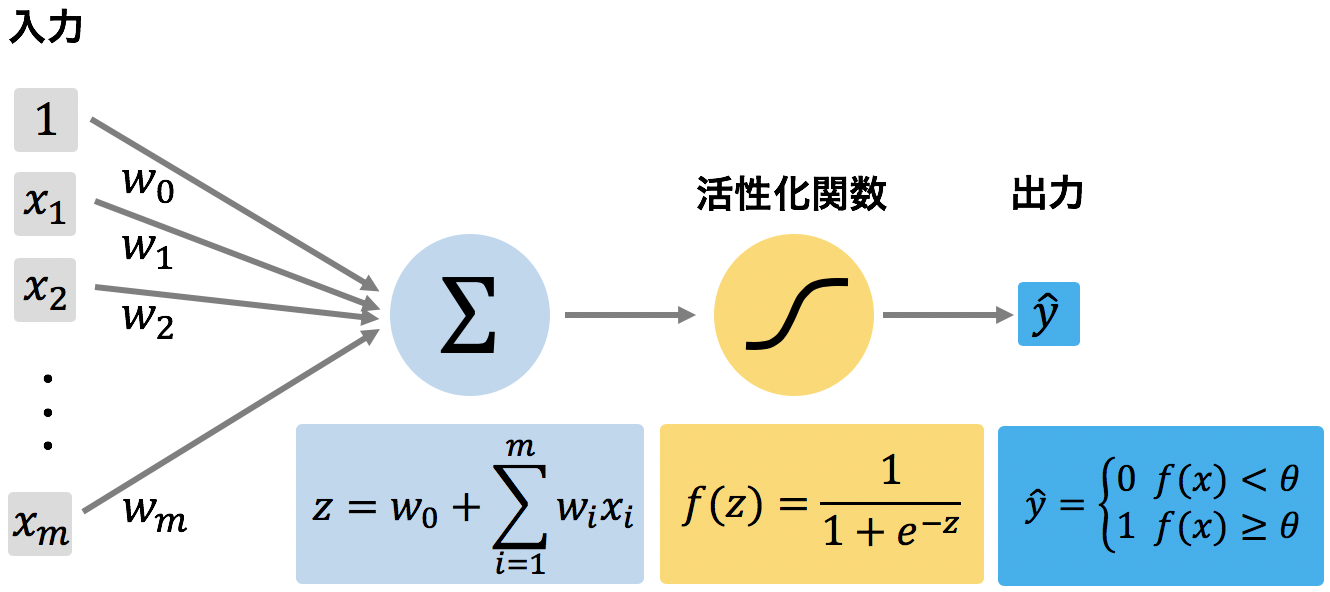
ロジスティックシグモイド関数
確率(0≤p≤1)をモデリングするときにロジット関数が一般的に使われている。ロジット関数は、0 から 1 までの値をとる確率 p を受け取り、マイナス無限大からプラス無限大までの実数値を返す関数である。
\[ logit(p(y=1|\mathbf{x})) = \log \frac{p(y=1|\mathbf{x})}{1-p(y=1|\mathbf{x})} \]このロジット関数の逆関数(ロジスティックシグモイド関数)を使用することで、任意の実数値 z を 0 から 1 までの値に写像することができる。
\[ z = \log \frac{p(y=1|\mathbf{x})}{1-p(y=1|\mathbf{x})} \Longleftrightarrow p(y=1|\mathbf{x}) = \frac{1}{1+e^{-z}} \]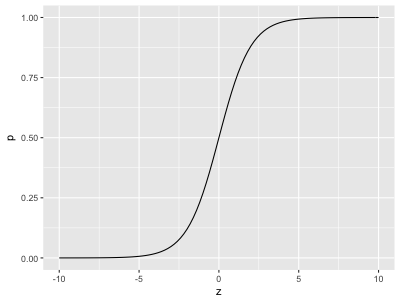
このロジスティックシグモイド関数を用いることで、特徴量ベクトル x とウェイト w の内積を確率に変換できる。そして、ロジスティックシグモイド関数の出力値が 0.5 以上であれば 1 を、そうでなければ 0 を出力するように決めることで、二値予測のモデルを作成できるようになる。
\[ f(z) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\mathbf{w}^{T}\mathbf{x}}} \] \[ \begin{eqnarray} \hat{y} = \begin{cases} 1 & ( f(z) \ge 0.5 ) \\ 0 & ( f(z) \lt 0.5 ) \end{cases} \end{eqnarray} \]損失関数
尤度関数
ある x を与えたとき、y = 1 が得られる確率はロジスティックシグモイド関数 f(x) で表されるとする。このとき、y = 1 となる確率は f(x) であり、y = 0 となる確率は 1 - f(x) である。n 個の学習データセット (X, y) が与えられたとき、その n 個のデータセットが同時に観測できる確率は次のように書ける。これを尤度関数という。
\[ L(\mathbf{y} | \mathbf{X}, \mathbf{w}) = \prod_{i=1}^{n}p(y^{(i)}|x^{i}, \mathbf{w}) = \prod_{i=1}^{n}\left(f(z^{(i)})\right)^{y^{(i)}}\left(1-f(z^{(i)})\right)^{1-y^{(i)}} \]予測モデルを作成するとき、x にウェイト w をかけて、その値をできるだけ y に近づけることである。つまり、観測された n 個のデータセットがあったとき、X にウェイト w をかけて、できる限り y に近づけるような w を求めればよい。この問題は、尤度関数の最大化問題に帰着することができる。
尤度関数は、複数の確率の積からなるので、実際に計算すると非常に小さな値となる。プログラムなどで計算すると、桁落ちなどが生じたりして正確さが欠ける。そこで、この尤度関数を最大化する代わりに、対数化した対数尤度関数を最大化するのが一般的である。
\[ l(\mathbf{y} | \mathbf{x}, \mathbf{w}) = \sum_{i=1}^{n}\left\{ y^{(i)}\log \left( f(z^{(i)}) \right) + (1-y^{(i)})\log \left(1-f(z^{(i)}) \right) \right\} \]損失関数
w を求めるのに、対数尤度関数を最大化する w を求めればよい。これを損失関数として利用する場合は、対数尤度関数に -1 をかければよい。
\[ loss(\mathbf{w}) = - l(\mathbf{y} | \mathbf{x}, \mathbf{w}) = - \sum_{i=1}^{n}\left\{ y^{(i)}\log \left( f(z^{(i)}) \right) + (1-y^{(i)})\log \left(1-f(z^{(i)}) \right) \right\} \]この損失関数の最小値を求めるには、勾配降下法などが利用できる。
\[ \mathbf{w}^{new} = \mathbf{w} \Delta \mathbf{w} \] \[ \Delta \mathbf{w} = - \eta \nabla loss(\mathbf{w}) \]