分類問題を解く教師あり機械学習のアルゴリズム
決定木
決定木 decision tree は、分類問題と回帰問題を解く教師あり学習のアルゴリズムの一つである。与えられたデータに対して、次々に条件を設けて、データを段階的に分類していく手法である。解析結果は、直感的に解釈しやすいのが特徴である。例えば、植物を分類する際には、下図のような決定木を作ることができる。
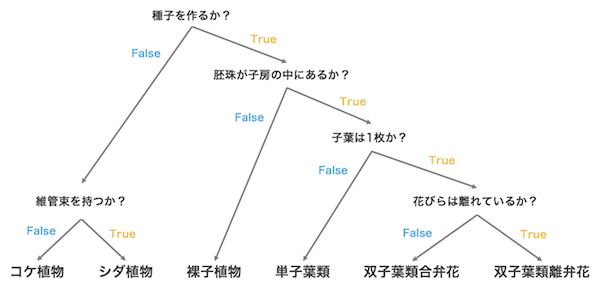
決定木を作る流れとして、情報利得を最大となるように、データを複数のカテゴリに分割する。次に、それぞれのカテゴリに対して、再度、情報利得が最大となるようにデータを分割する。このような作業を適切な回数で繰り返すことで、決定木が作られる。
決定木を作成するときに、枝の分割条件が数値の大小比較となるので、特徴量を標準化する必要はない。特徴量を標準化するとしないで、分割条件の閾値の大きさが変化するが、結果に何ら影響も及ぼさない。
プログラミング言語
情報利得
1 つのノードに異なるクラスのサンプルが含まれる割合を数値化した値を不純度という。1 つのノードに含まれるサンプルが複数のクラスに由来しているものであれば、そのノードの不純度は大きい。逆に、1 つのノードに含まれるサンプルが 1 つのクラスだけに由来していれば、そのノードの不純度は小さい。
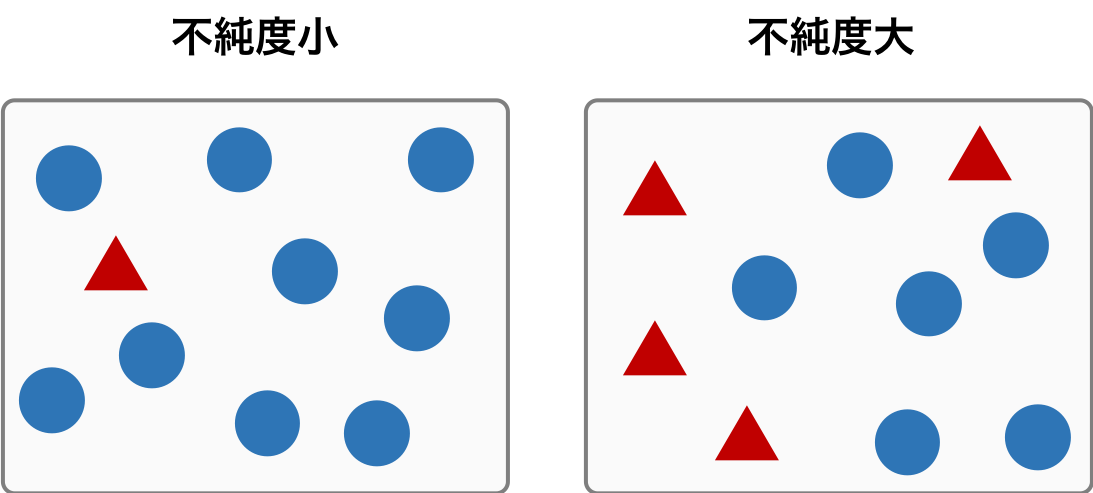
情報利得は、親ノードの不純度とその子ノードの不純度の差を表す。親ノードの不純度が大きく、子ノードの不純度が小さいとき、情報利得が最も大きくなる。つまり、親ノードには様々なクラスに由来するサンプルが含まれ、それらのサンプルが正確に子ノードに振り分けているとき、情報利得が最も大きくなる。
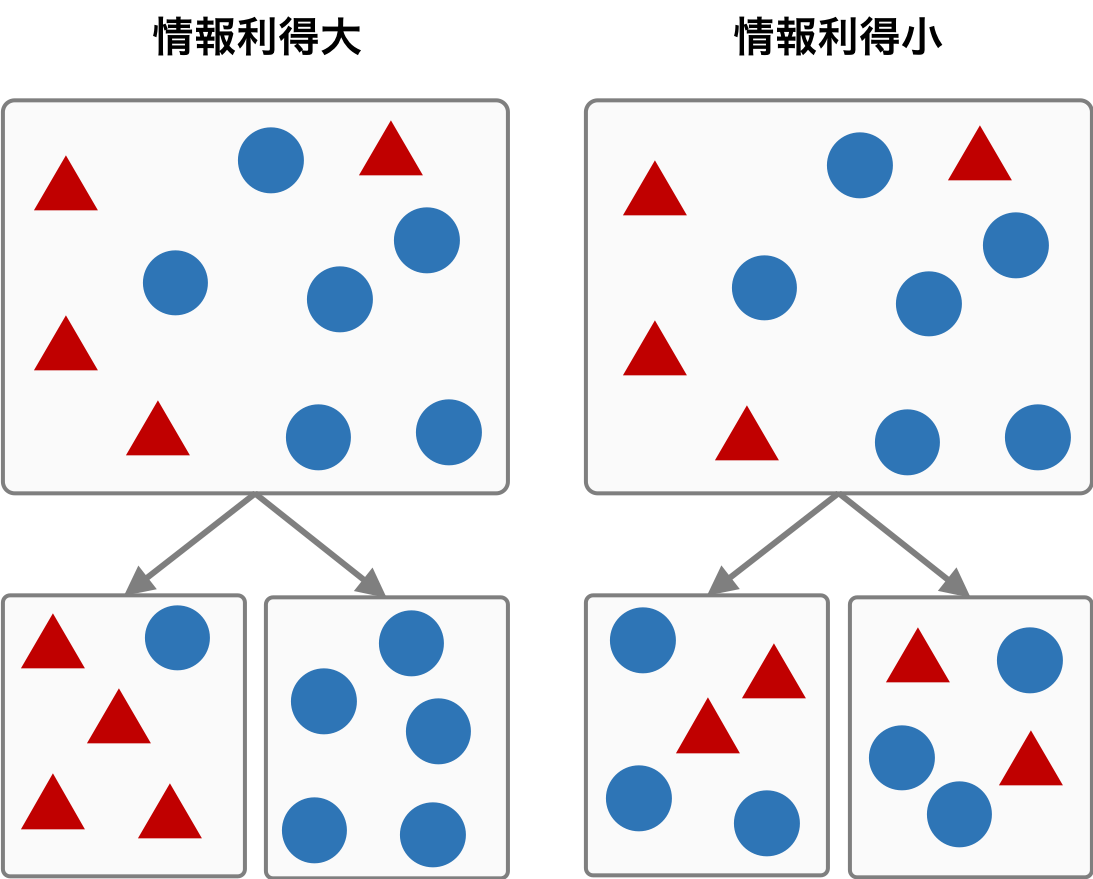
あるノード j の不純度を I(Dj) とかくと、情報利得 IG は、親ノードの不純度 I(Dp) と子ノードの不純度 I(Dj) (j = 1, 2, 3, ..., c) を用いて次のように書き表すことができる。ただし、Np は親ノードに含まれるサンプルサイズを表し、Nj は j 番目の子ノードに含まれるサンプルサイズをとする。また、1 つの親ノードからは c 個の子ノードが作られるものとする。
\[ IG(D_{p}) = I(D_{p}) - \sum_{j=1}^{c}\frac{N_{j}}{N_{p}}I(D_{j}) \]不純度
不純度を測る指標として、エントロピー IH、ジニ不純度 IG、または分類誤差 IE が用いられる。一般的に用いられる不純度は、エントロピー IH とジニ不純度 IG である。この両者はほぼ同じような結果が得られると言われている。
エントロピー
エントロピーは、一般的に乱雑さを測る指標として用いられる。ノード t に含まれるクラス c に属するサンプルの割合を p(t|c) とおくと、ノード t におけるエントロピーは次のように書ける。
\[ I_{H}(t) = - \sum_{c=1}^{C}p(c|t)\log_{2}p(c|t) \]ノード t に含まれるサンプルの全てが同じクラス j に由来する場合、p(c=j|t) = 1 かつ p(c≠j|t) = 0 であるので、エントロピーはゼロとなる。また、ノード t に含まれるサンプルが全てのクラス c = 1, 2, 3, ..., C に同数ずつ由来していれば、p(c=1|t) = p(c=2|t) = ... = p(c=C|t) = 1/C となるので、エントロピーは log2C となる。
ジニ不純度
ジニ不純どは次のように定義されている。この式から、ジニ不純度はエントロピーと似た結果が得られることがわかる。
\[ I_{G} = \sum_{c=1}^{C} p(c|t)(1 - p(c|t)) = 1 - \sum_{c=1}^{C}p(c|t)^{2} \]分類誤差
分類誤差は次のように定義されている。
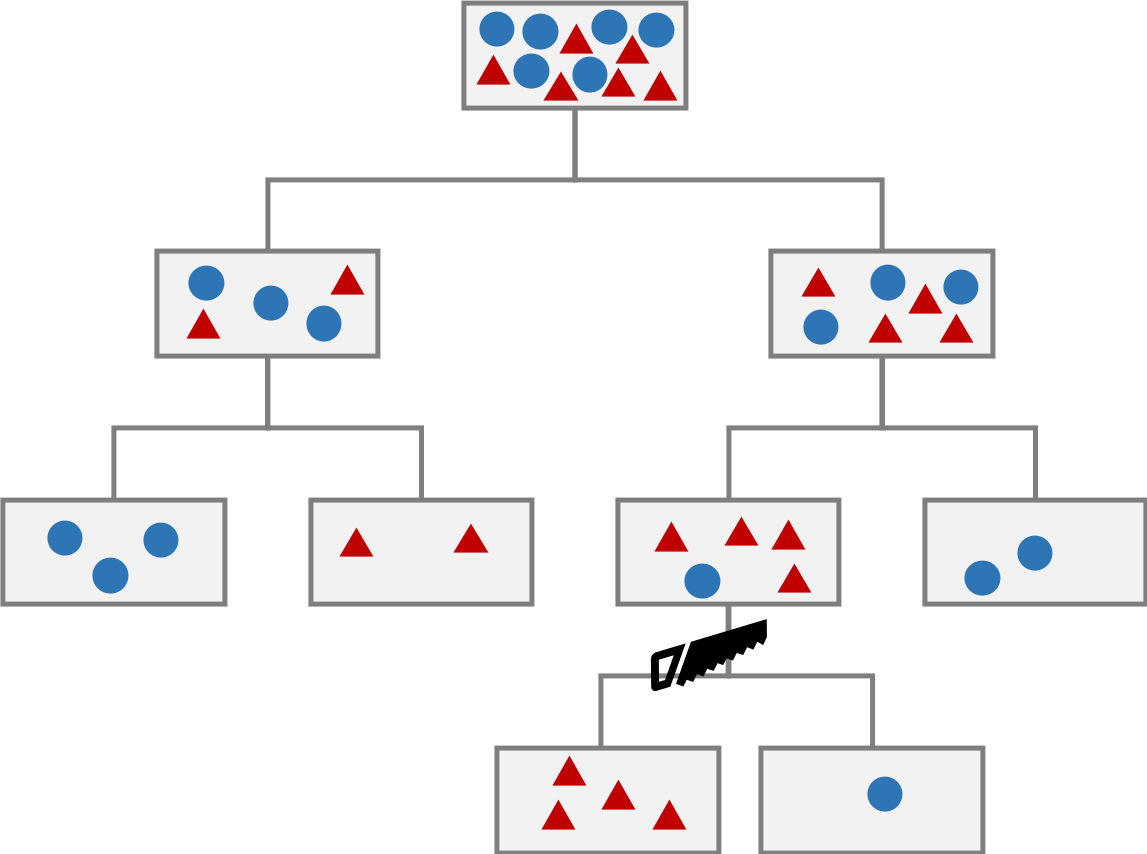
\[ I_{E}(t) = 1 - \max\{p(c|t)\} \]剪定
決定木の枝数(層数)を増やことで、すべての訓練データを間違いなく分類できるようになる。訓練データに含まれるノイズまでも分類対象となってしまうことがある。この状態を過学習という。過学習を防ぐために、剪定(枝刈り)を行い、枝数を制限することが行われている。剪定は、例えば、情報利得が閾値以下であれば、そこで剪定する。あるいは、決定木全体の複雑性が小さくなるように剪定するなどの方法がある。