階層的クラスタリングは、要素間の類似度(距離)に基づいて、最も似ている要素から順次に集めてクラスターを作っていく方法である。具体的な手順としては、次のようになる。
- N 個の要素が与えられたとき、これらを N 個のクラスターと仮定して(各クラスターには 1 要素だけを含む)、クラスター間の距離を計算する。
- 距離がもっとも近い 2 つのクラスターをまとめて、1 つのクラスターとする。N 個のクラスターが、N - 1 個になる。
- N - 1 個のクラスター間の距離を計算して、手順 2 に進む。クラスター数が 1 個になるまで、手順 2-3 を繰り返す。
クラスター間の距離を計算するには、最短距離法、群平均法やウォード法などがある。
最短距離法 / 単連結法
クラスター C1 とクラスター C2 のそれぞれに複数の要素が含まれるとき、C1 と C2 の距離 d(C1, C2) が、そのクラスターに含まれる要素同士の中で、距離のもっとも近い要素間の距離をクラスター距離とする計算手法が、最短距離法である。最短距離法によるクラスタリングは、外れ値に弱く、クラスターが帯状になりやすい(鎖効果)ため、分類感度が低い。
\[ d(C_{1}, C_{2}) = \min_{x_{1}\in C_{1}, x_{2}\in C_{2}}d(x_{1}, x_{2}) \]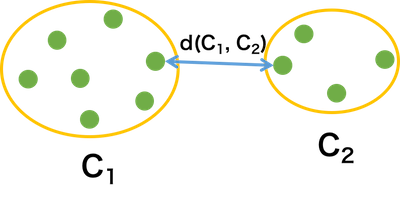
最長距離法 / 完全連結法
クラスター C1 とクラスター C2 のそれぞれに複数の要素が含まれるとき、C1 と C2 の距離 d(C1, C2) が、そのクラスターに含まれる要素同士の中で、距離のもっとも遠い要素間の距離をクラスター距離とする計算手法が、最長距離法である。最長距離法によるクラスタリングは、外れ値に弱く、クラスター同士が離れてしまう性質を持つ(拡散効果)。しかし、各クラスターのサイズが揃いやすく、分類感度は、最短距離法より優れている。
\[ d(C_{1}, C_{2}) = \max_{x_{1}\in C_{1}, x_{2}\in C_{2}}d(x_{1}, x_{2}) \]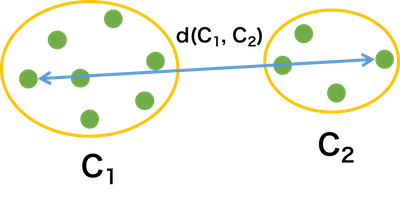
群平均法
2 つのクラスターに含まれているすべての要素に対して、要素間の距離を求めて、それらの平均をクラスター間の距離とする計算手法である。外れ値に強く、鎖効果や拡散現象を起こしにくい。
\[ d(C_{1}, C_{2}) = \frac{1}{|C_{1}||C_{2}|}\sum_{x_{i} \in C_{1}}\sum_{x_{j} \in C_{2}} d(x_{i}, x_{j}) \]
ウォード法(Ward's method)
クラスター C1 とクラスター C2 を仮に 1 つのクラスターにまとめたとき、そのクラスター重心と各要素間の距離の 2 乗和(E(C1∪C2))から、もとのクラスター C1 と C2 の重心と各要素の距離の 2 乗和を引いた値をクラスター距離とする手法である。外れ値に弱いが、群平均法などに比べて分類感度が良く、一般的によく使われている。
\[ d(C_{1}, C_{2}) = E(C_{1} \cup C_{2}) - E(C_{1}) - E(C_{2}) \] \[ E(C_{i}) = \sum_{x \in C_{i}}\left( d(x, \mu_{i}) \right)^{2} \] \[ \mu_{i} = \sum_{x \in C_{i}} \frac{x}{|C_{i}|} \]重心法
2 つのクラスターの重心の間の距離の 2 乗を、クラスター距離とするクラスタリング手法である。
メディアン法
2 つのクラスターの重心に、クラスタ内の要素数を重みとして乗じた値をクラスター距離とするクラスタリング手法である。