LSTM (Long short-term memory) は、長期記憶を可能にした再帰型ニューラルネットワークの一つである。通常の RNN は勾配を逆伝播することによって学習を行うが、状態 t が長くなると、その勾配が消失したりあるいは発散したりすることが指摘された。そのため、通常の RNN は、長期記憶に依存する系列データの学習が正しく行われないことがわかってきた。この問題を解決するためのアルゴリズムの一つとして、LSTM が提唱された。LSTM は、セルの内部(LSTM ブロック)において、情報を長期的に保存するための変数が設けられている。そして、この変数に対して、古くなった情報を削除したり、新しい情報を足したりして、適当な長期記憶を可能にしている。LSTM は、現在、翻訳、音声認識、キャプション生成などに応用されている。
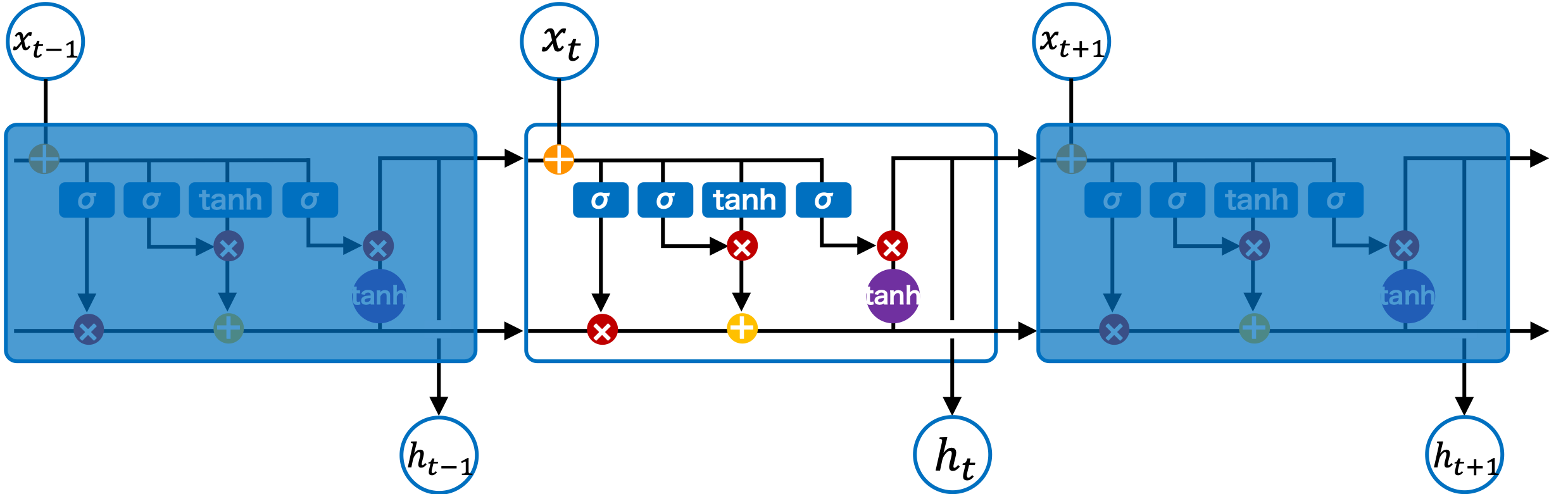
LSTM ブロックの構造
通常の RNN では、データは入力層、中間層、出力層の順で伝播され、結果が出力される。LSTM もこれと同じ仕組みで、データは入力層、中間層、出力層の順で伝播される。しかし、RNN の中間層はニューラルネットワークと同様に活性化関数が 1 つだけであるのに対して、LSTM の中間層には複数の活性化関数が用意され、複雑な演算が行われている。LSTM の中間層における演算部分をセルと呼んだり、LSTM ブロックと呼んだりする。
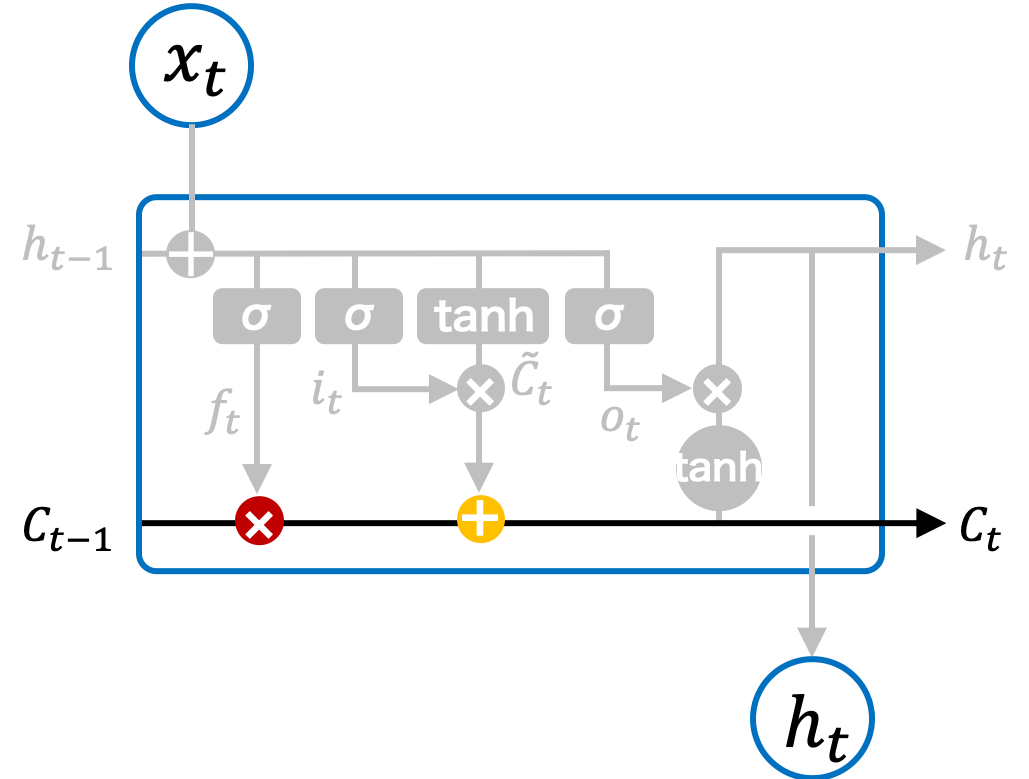
長期記憶
LSTM ではセルの長期記憶を保つための変数 Ct が用意されている。長期記憶 Ct に対して、古くなった記憶を削除したり、新しい情報を新規追加したりすることで、適当な長期記憶を可能にしている。具体的には、数のように、一つの前の状態から伝達された長期記憶 Ct-1 に対して、0 から 1 での割合をかけて、古い記憶を何割か忘れさせる。次に、入力および現在の状態から得られた新しい情報を長期記憶に追加する。次に、この状態で得られた長期記憶を次の状態に伝達する。
忘却ゲート
LSTM の忘却ゲートでは、長期記憶から情報を忘却するための制御を行っている。入力 xt と一つ前のセルの出力値 ht-1 を受け取り、記憶率 ft を計算する。ft の各要素はシグモイド関数によって計算されるため、0 以上かつ 1 以下の値をとる。
\[ \mathbf{f}_{t} = \sigma \left( \mathbf{W}_{f} \mathbf{x}_{t} + \mathbf{U}_{f} \mathbf{h}_{t-1} + \mathbf{b}_{f} \right) \]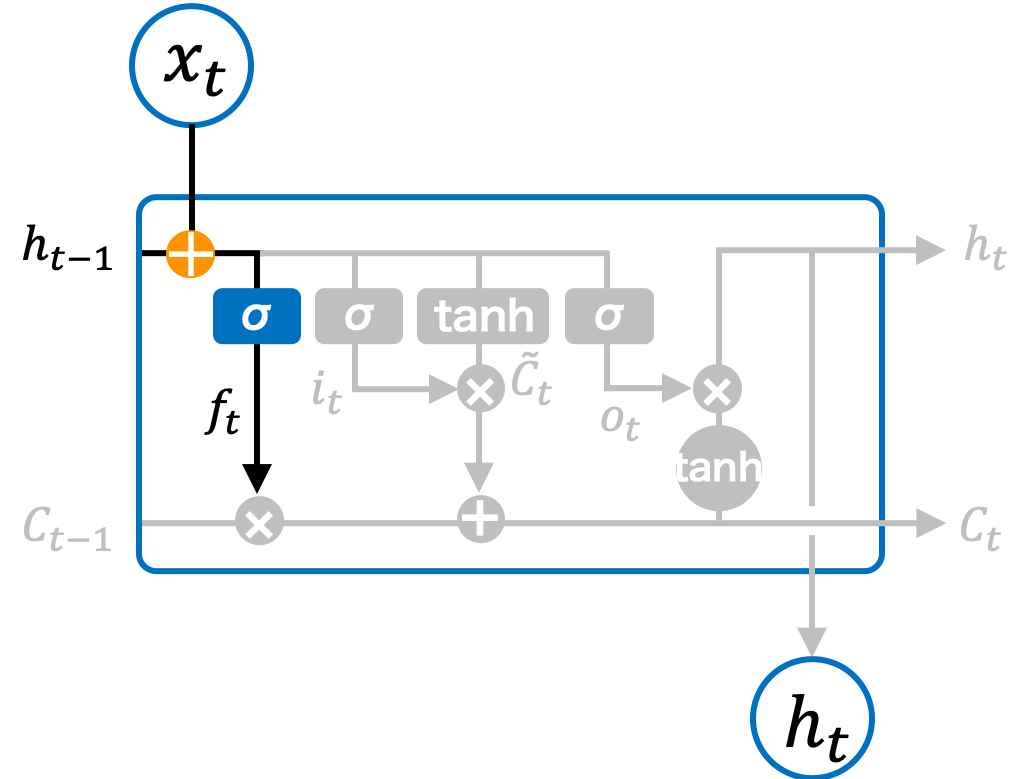
ft は、一つ前のセルの長期記憶 Ct にかかるため、Ct をどのぐらい記憶しつづけるのかを制御する係数とみなすことができる。 Ct のある要素 Cj にかかる fj が 1.0 ならば、その要素の記憶を保ったままで処理を続けるが、fj = 0.2 ならば、その要素の情報を 80% 忘れてから処理を続けることになる。
入力ゲート
次に、通常の RNN と同様に、入力 xt と一つ前のセルの出力値 ht-1 を受け取り、現在のセルの状態 \( \tilde{\mathbf{C}}_{t} \) を計算する。この値が、長期記憶に保存する候補となる。
\[ \tilde{\mathbf{C}}_{t} = \tanh \left( \mathbf{W}_{C} \mathbf{x}_{t} + \mathbf{U}_{C} \mathbf{h}_{t-1} + \mathbf{b}_{C} \right) \]\( \tilde{\mathbf{C}}_{t} \) の情報すべてを長期記憶に留める必要はなく、必要な情報だけを長期記憶に留めるた方が効率よい。そこで、\( \tilde{\mathbf{C}}_{t} \) の情報に記憶率 it をかける計算を行えば良い。その記憶率 it は、入力 xt と一つ前のセルの出力値 ht-1 から計算する。it はシグモイド関数によって計算されるため、その各要素は 0 以上かつ 1 以下の値をとる。
\[ \mathbf{i}_{t} = \sigma \left( \mathbf{W}_{i} \mathbf{x}_{t} + \mathbf{U}_{i} \mathbf{h}_{t-1} + \mathbf{b}_{i} \right) \]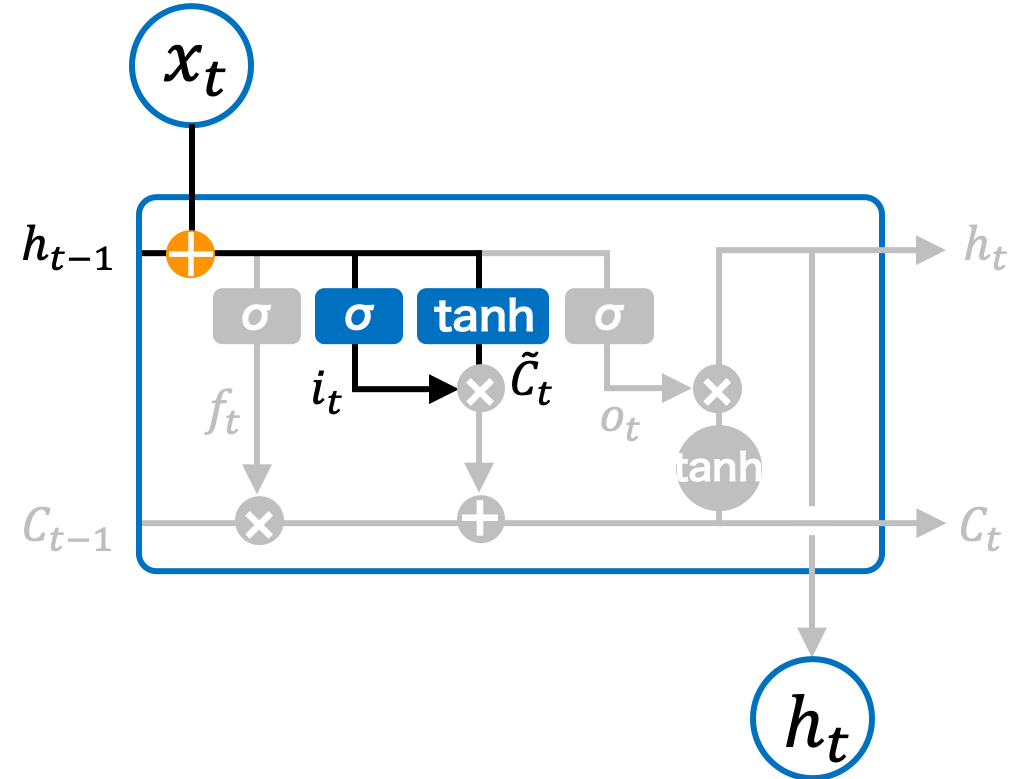
長期記憶の更新
一つ前のセルの長期記憶 Ct-1 に対して、適宜に記憶を忘却してから、そこに、新しい入力に基づいて計算される情報を足して、最新の長期記憶 Ct とする。なお、丸中点 ⊙ は、同じサイズの行列の成分同士の積(アダマール積)を表す。
\[ \mathbf{C}_{t} = \mathbf{f}_{t} \odot \mathbf{C}_{t-1} + \mathbf{i}_{t} \odot \tilde{\mathbf{C}}_{t} \]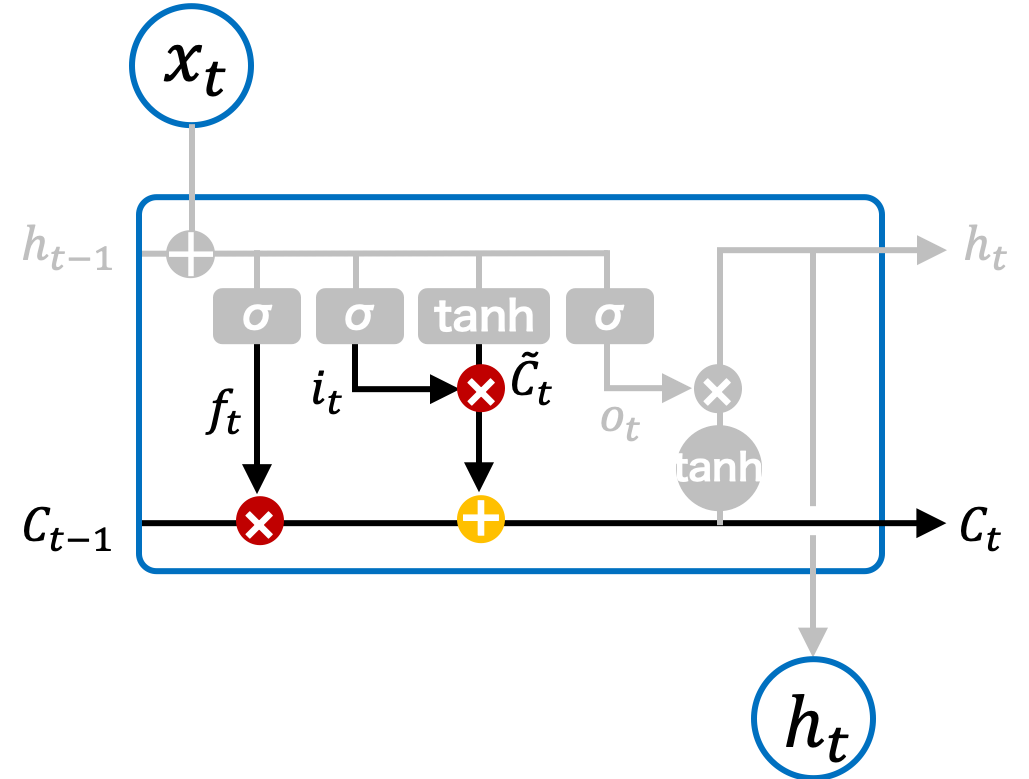
出力ゲート
状態 t のセルにおける出力値は、入力情報 xt と ht-1 を基にして、現在の長期記憶に保存されている情報を加えて、値を出力する。
\[ \mathbf{o}_{t} = \sigma \left( \mathbf{W}_{o} \mathbf{x}_{t} + \mathbf{U}_{o} \mathbf{h}_{t-1} + \mathbf{b}_{o} \right) \] \[ \mathbf{h}_{t} = \mathbf{o}_{t} \odot \tanh \mathbf{C}_{t} \]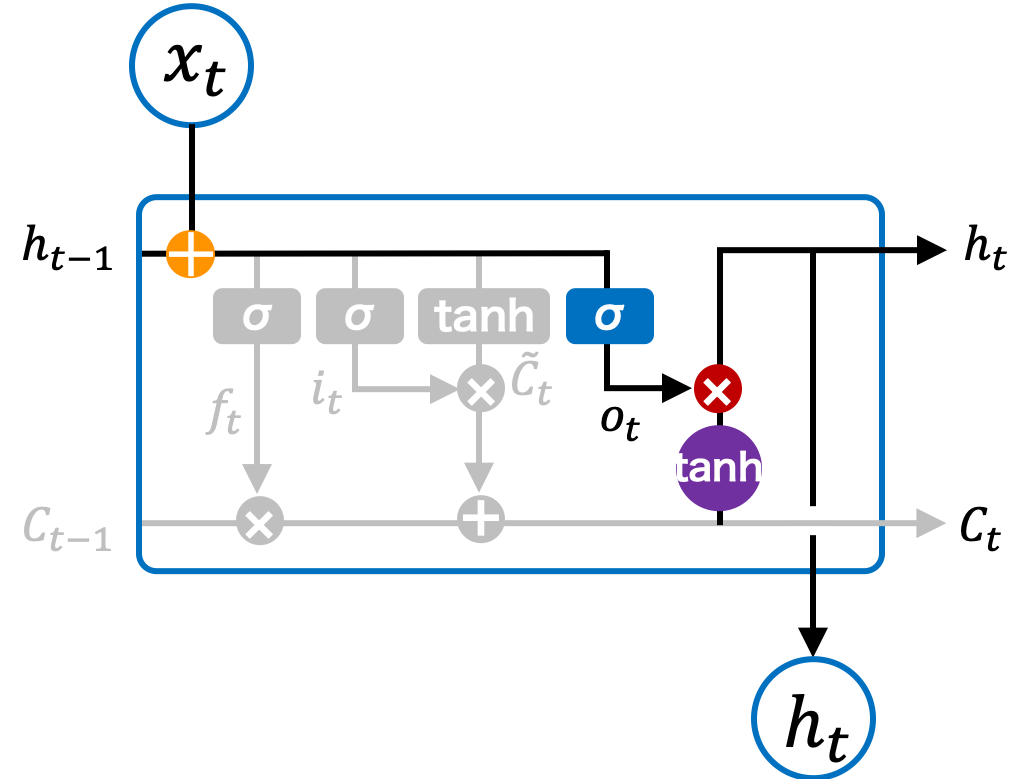
References
- Understanding LSTM Networks. 2015. colah's blog