単純パーセプトロン

パーセプトロンは、複数のシグナルを受け取り、1 つのシグナルを出力する。パーセプトロンは、以下のように入力データ x = (x₁, x₂, ..., x_m) を受け取り、受け取った各特徴量に対してウェイト w = (w₁, w₂, ..., w_m) をかけて合計を計算する。そして、その合計値に定数項 w₀ を加えて（z = w₀ + Σw_ix_i）、活性化関数に代入する。活性化関数は、z を受け取り、z > θ ならば 1 を出力し、そうでなければ 0 を出力する。

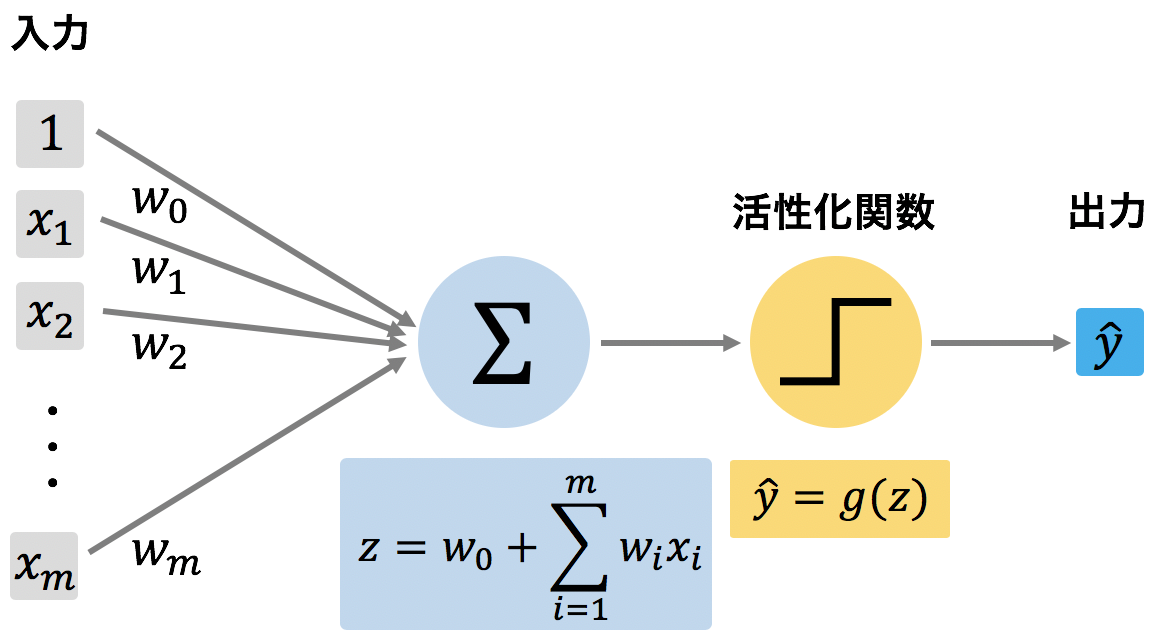
パーセプトロンを数式で表すと次のようになる。ただし、下記の例では、活性化関数 g(z) をステップ関数としたので、z > 0 かどうかで出力が 1 または 0 となっている。実際には、活性化関数にシグモイド関数や ReLU 関数などを用いると、g(z) の出力値は 0 または 1 以外の値も取りうる。

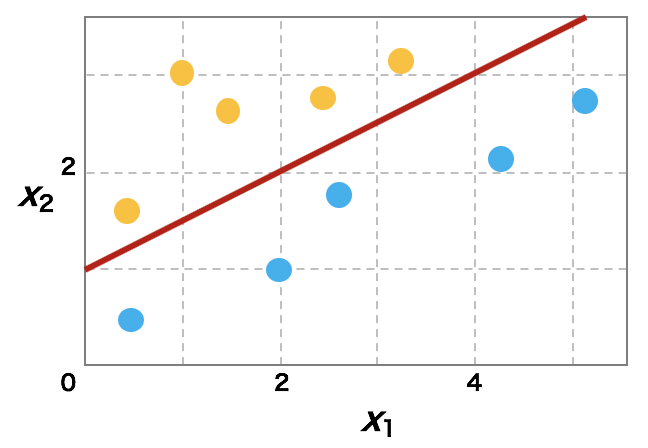
パーセプトロンを利用した機械学習では、学習データである (y, x) を入力し、y^{^}   (= g(z)) が y との誤差がもっとも小さくなるような w を求めることである。例えば、イメージとして、以下のような二次元の特徴量を持つオレンジ色と水色の点を分けるには、ウェイト w として、 (w₀, w₁, w₂) = (-1, -0.5, 1) が解の一つとして求まる。このとき、(x₁, x₂) = (1, 3) ならば、z = -1 - 0.5×1 + 1×3 = 1.5 > 0 なので、オレンジと分類される。また、(x₁, x₂) = (2, 1) ならば、z = -1 - 0.5×2 + 1 = -1 ≤ 0 なので水色と分類される。

学習を通して求めたウェイト w の値は、パーセプトロンの学習アルゴリズムによって異なる場合がある。また、学習データの入力順序によってもウェイト w の値が変化する場合もある。

また、この例で見たように、パーセプトロンは、線形的によく分離しているデータに対して有効である。しかし、データが線形的に分離していないときに、パーセプトロンはその効力を発揮できない。

多層パーセプトロン

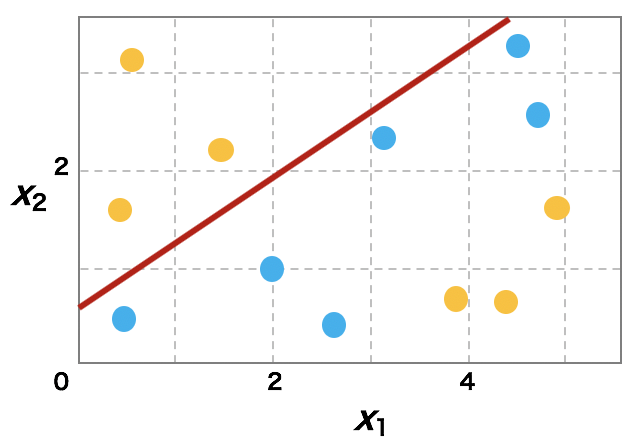
単一のパーセプトロンはデータを線形的にしか分類できない。しかし、複数のパーセプトロンを適当につなげることで、線形分離できないデータも分離できるようになる。例えば、下図のような線形では分類できないデータに対して、2 つのパーセプトロンを用意して、両者の結果を合わせることで、データを分類できるようになる。

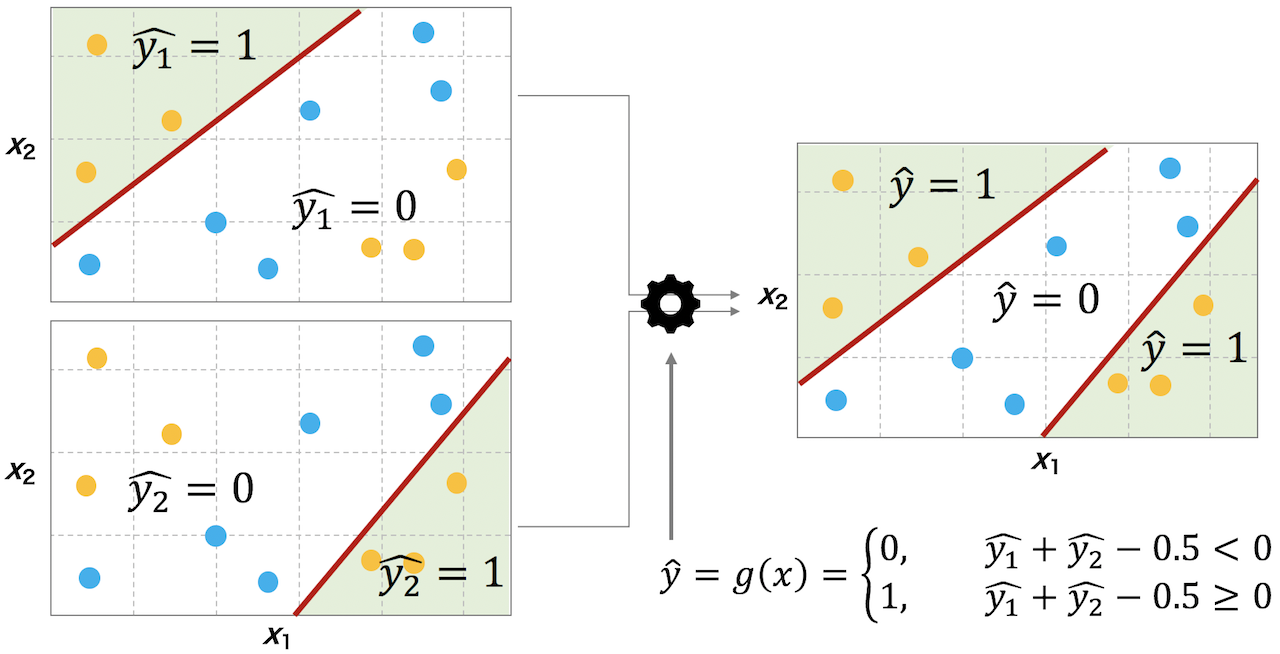
上図の例では、まず 1 つのパーセプトロンにより平面を g(z₁) = 1 と g(z₁) = 0 の 2 つの領域に分ける。続いて、もう 1 つのパーセプトロンを用意して画面をもう一度 g(z₂) = 1 と g(z₁) = 0 の 2 つの領域に分ける。そして、この 2 つのパーセプトロンの出力結果 g(z₁) と g(z₂) を 3 つ目のパーセプトロンに代入し、両者の和が 0 から 0.5 を引き、その結果が 0 以上ならばオレンジ色、0 未満であれば青色を出力する。

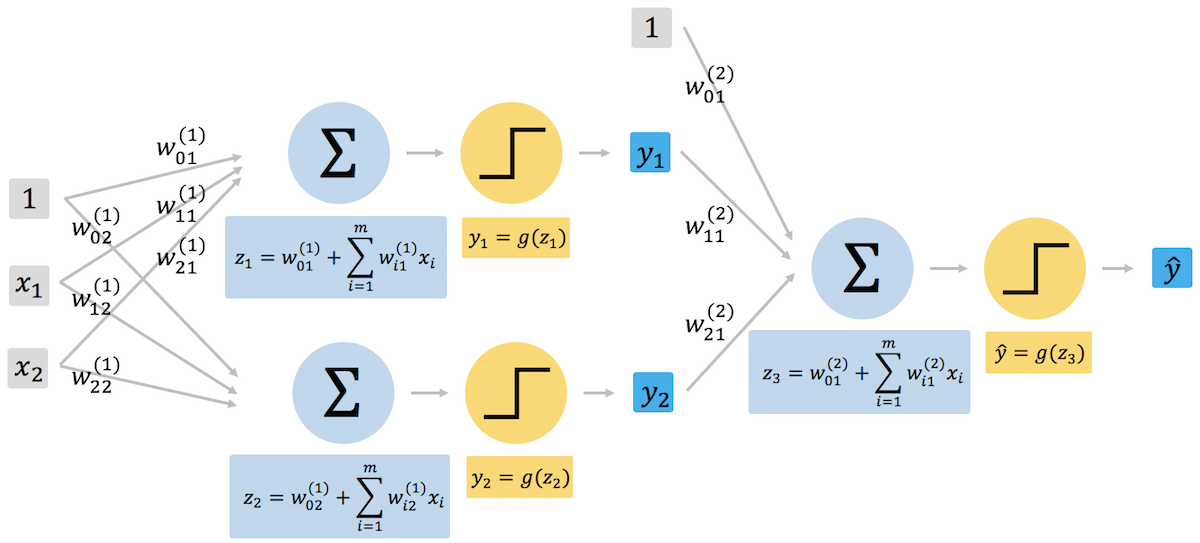
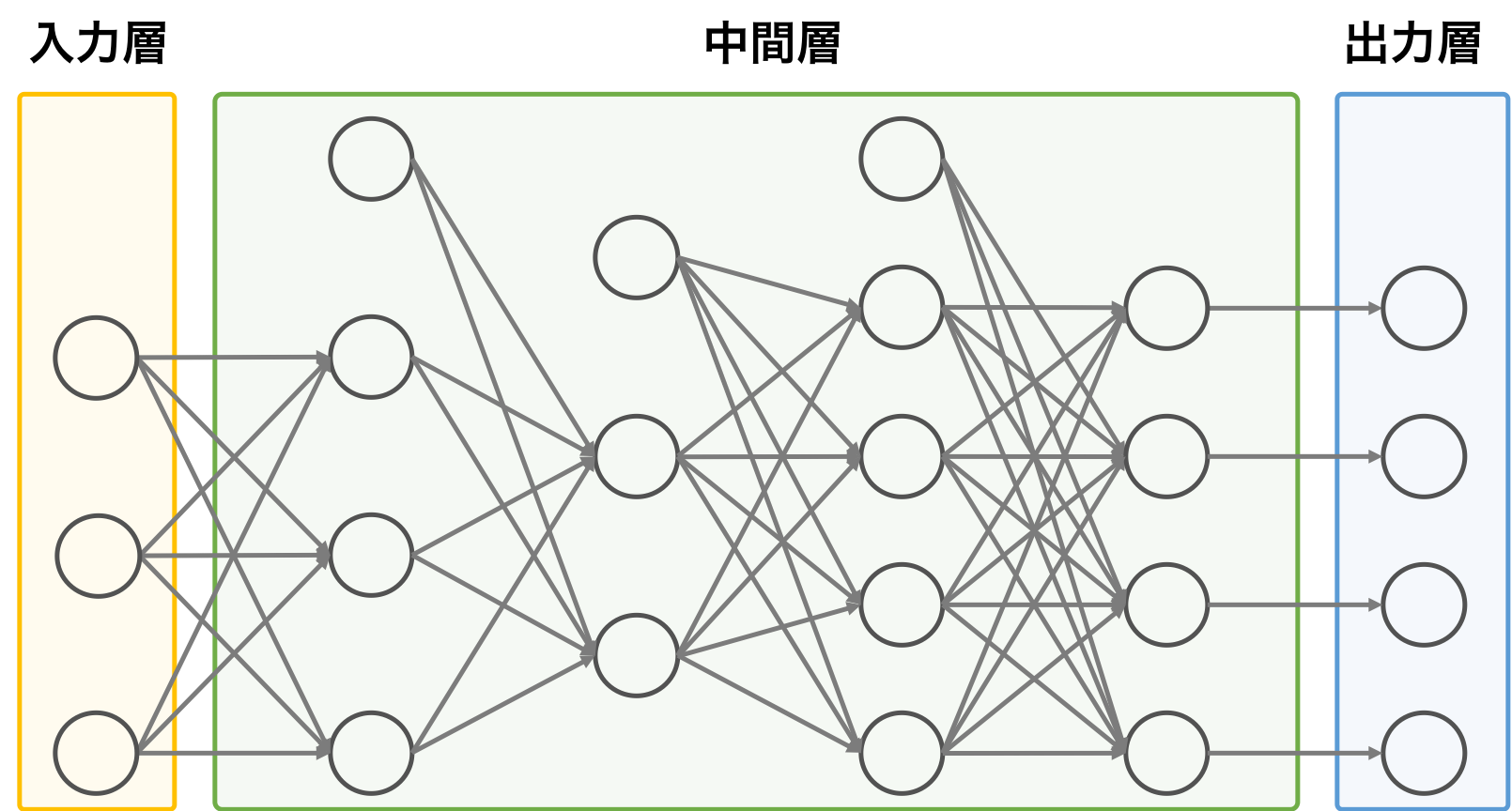
ニューラルネットワーク

パーセプトロンの数および層の数を増やすことで、線型的に分離できないデータをも分類できるようになる。このようなパーセプトロンを複数つなげたモデルをニューラルネットワークという。ニューラルネットワークは、パーセプトロンが複数の層で繋がっているので、それぞれの層の特徴に応じて、入力層、中間層、および出力層に分けることができる。

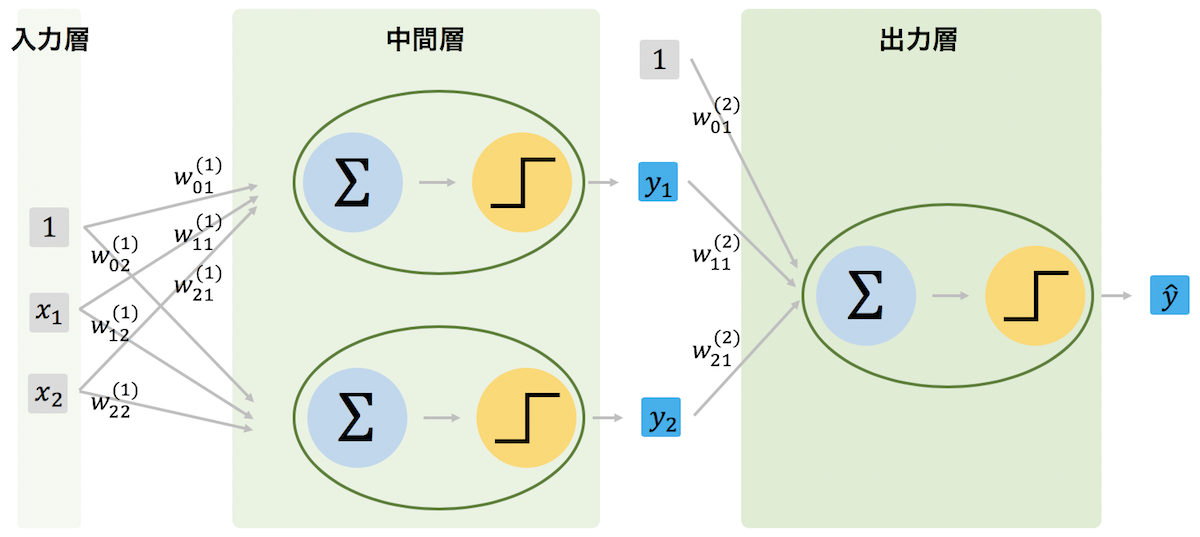
また、中間層において、層の数を増やすことによって、ディープニューラルネットワーク（DNN）を実現することができる。この概念・手法が深層学習として使われている。