ニューラルネットワークの出力層を 1 ユニットにすることで、回帰問題に利用できる。このページでは、ニューラルネットワークを使用して、1 つの特徴量で、1 つの目的変数を予測する回帰問題の例を示す。

ここで乱数を使用して特徴量 x と教師ラベル y を作成する。

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(2020)

x = np.random.uniform(0, 10, 100)
y = np.sin(x) + np.random.uniform(-0.5, 0.5, 100)

fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(x, y)
ax.set_xlabel('x')
ax.set_xlabel('y')
fig.show()

続いて、PyTorch でニューラルネットワークを定義する。ここでは、入力層 (1 unit)、中間層 (128 units)、中間層 (64 units)、および出力層 (1 unit) の 4 層からなる簡単なニューラルネットワークを定義している。このネットワークを定義するとき、初めは中間層を 1 層だけで設計していたが、うまくフィッティングできなかったために、この例では中間層を 2 層にした。

import torch
import torch.nn.functional
import torch.utils.data


class Net(torch.nn.Module):

  def __init__(self):
    super(Net, self).__init__()
    self.fc1 = torch.nn.Linear(1, 128)
    self.fc2 = torch.nn.Linear(128, 64)
    self.fc3 = torch.nn.Linear(64, 1)

  def forward(self, x):
    x = torch.nn.functional.relu(self.fc1(x))
    x = torch.nn.functional.relu(self.fc2(x))
    x = self.fc3(x)
    return x

上の定義に基づいてニューラルネットワークを構築し、学習データを代入して 1 万エポックで学習を進める。この際、損失関数を MSE とする。また、各エポックの訓練時における損失を epoch_loss に保存しておく。

num_epochs = 10000

# convert numpy array to tensor
x_tensor = torch.from_numpy(x.reshape(-1, 1)).float()
y_tensor = torch.from_numpy(y.reshape(-1, 1)).float()

# crate instance
net = Net()

# set training mode
net.train()

# set training parameters
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
criterion = torch.nn.MSELoss()

# start to train
epoch_loss = []
for epoch in range(num_epochs):
    # forward
    outputs = net(x_tensor)
    
    # calculate loss
    loss = criterion(outputs, y_tensor)
    
    # update weights
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    # save loss of this epoch
    epoch_loss.append(loss.data.numpy().tolist())

訓練時における損失 epoch_loss を図示して、学習が収束具合を確認する。およそ 1000 エポックぐらいで損失がほとんど減らなくなっている。

fig = plt.figure()
ax = fig.add_subplot()
ax.plot(list(range(len(epoch_loss))), epoch_loss)
ax.set_xlabel('#epoch')
ax.set_ylabel('loss')
fig.show()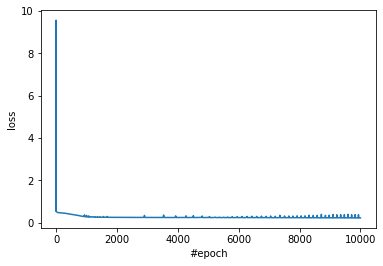

次に、訓練データの上に、ニューラルネットワークで予測した回帰曲線を描き込む。このために、0 から 10 までの範囲内で細かい間隔で等差数列を生成して x とし、これを上で学習したネットワークに代入して回帰曲線（回帰折れ線）を得る。そして、訓練データと回帰曲線を可視化する。

なお、ネットワークを検証・テストモードで使用するためには、ネットワークに対して eval() メソッドを実行する。今回の回帰の例は train() と eval() を使い分けなくてもよいが、ネットワーク中にバッチ正規化やドロップアウトなどを定義している場合に、切り替えが必要である。また、検証時に微分値でパラメーターの更新を行わないので、無駄な計算を行わないように torch.no_grad() の状態で検証する。

# set validaiton mode
net.eval()

# generate new 'x'
x_new = np.linspace(0, 10, 1000)
x_new_tensor = torch.from_numpy(x_new.reshape(-1, 1)).float()

# predict 'y'
with torch.no_grad():
    y_pred_tensor = net(x_new_tensor)

# convert tensor to numpy
y_pred = y_pred_tensor.data.numpy()


# plots
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(x, y)
ax.plot(x_new, y_pred, c='orange')
fig.show()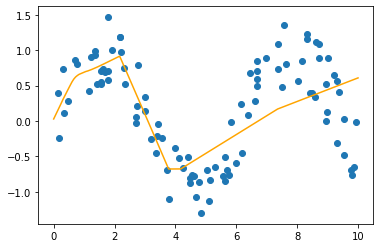

回帰曲線を見た感じから、訓練データの構造の複雑さに対して、ここで定義したニューラルネットワークがシンプルすぎる。それゆえ、一部がフィッティングされていない。中間層のユニット数を調整することで、ニューラルネットワークの表現力が上がり、より複雑なデータをも予測できるようになる。