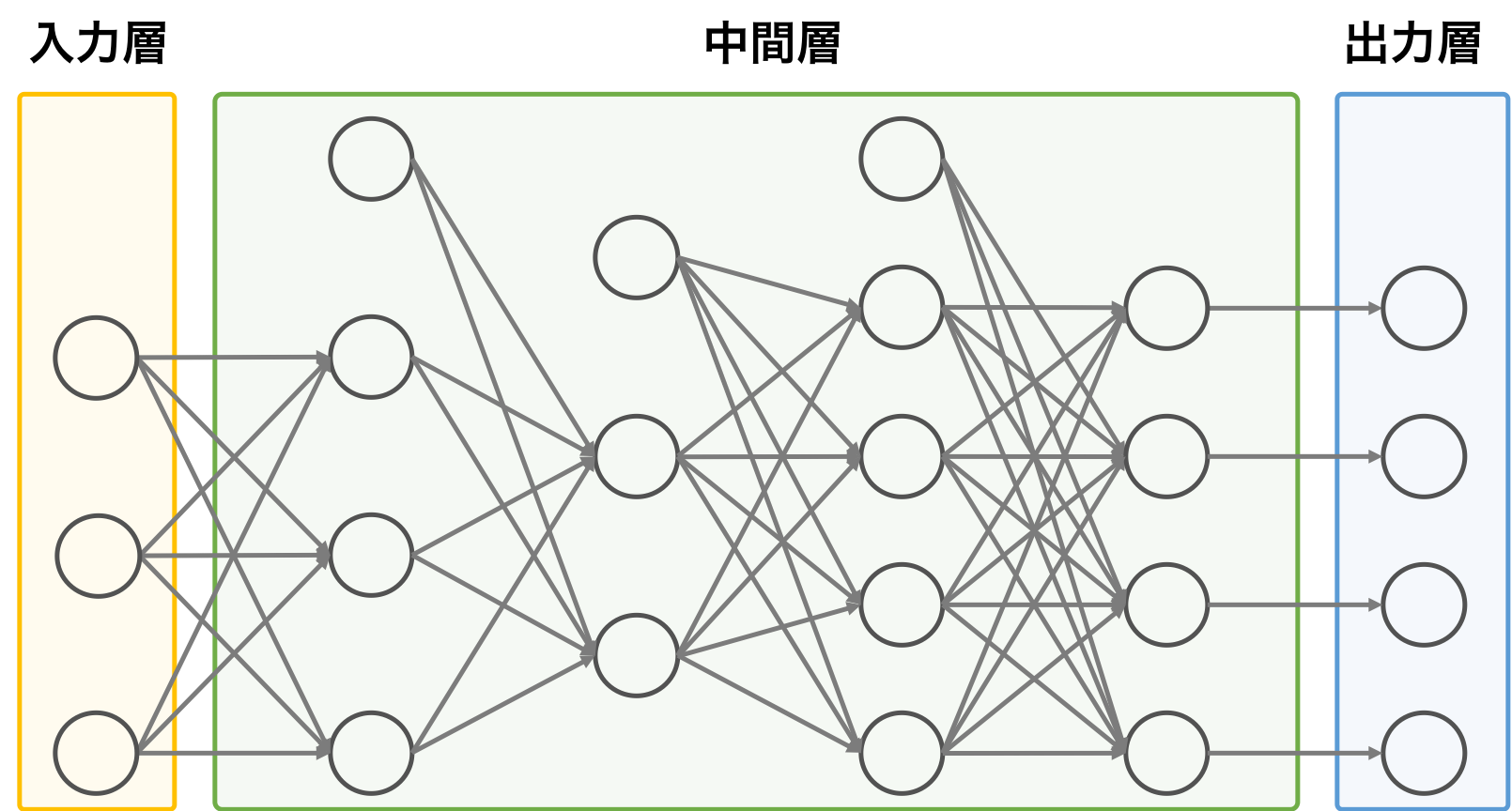
順伝播型ニューラルネットワークは、入力層、中間層、および出力層を含む。中間層が複数の層からなる場合もある。順伝播型ニューラルネットワークにおいて、情報の流れは、基本的に入力層から出力層の向けて流れ、逆方向への情報の伝播は行われない。ある層に存在しているユニットは、隣接する前の層のすべてのユニットの出力値を受け取り、演算を行ったあとに、その出力値を隣接する後の層にすべてのユニットに渡している。同一層の中でのユニット同士の接続はない。
順伝播型ニューラルネットワークの第 l 層には m 個のユニットがあり、m 個のユニットから出力される m 個の値をベクトル y(l) とおく。
\[ \mathbf{y}^{(l)} = \begin{pmatrix} y^{(l)}_{1} \\ y^{(l)}_{2} \\ \vdots \\ y^{(l)}_{m} \end{pmatrix} \]同様にして、第 l + 1 層には n 個のユニットがあるとして、n 個のユニットから出力される n 個の値をベクトル y(l+1) とおく。
\[ \mathbf{y}^{(l+1)} = \begin{pmatrix} y^{(l+1)}_{1} \\ y^{(l+1)}_{2} \\ \vdots \\ y^{(l+1)}_{n} \end{pmatrix} \]ニューラルネットワークでの情報の受け渡しついて、y(l+1) 層において、直前の層から出力された値 y(l) にウェイト w をかけてから合計値を計算した後に、バイアス w0 をさらに足した値 z を入力として受け取り、z を活性化関数に代入して出力値 y(l+1) を計算している。
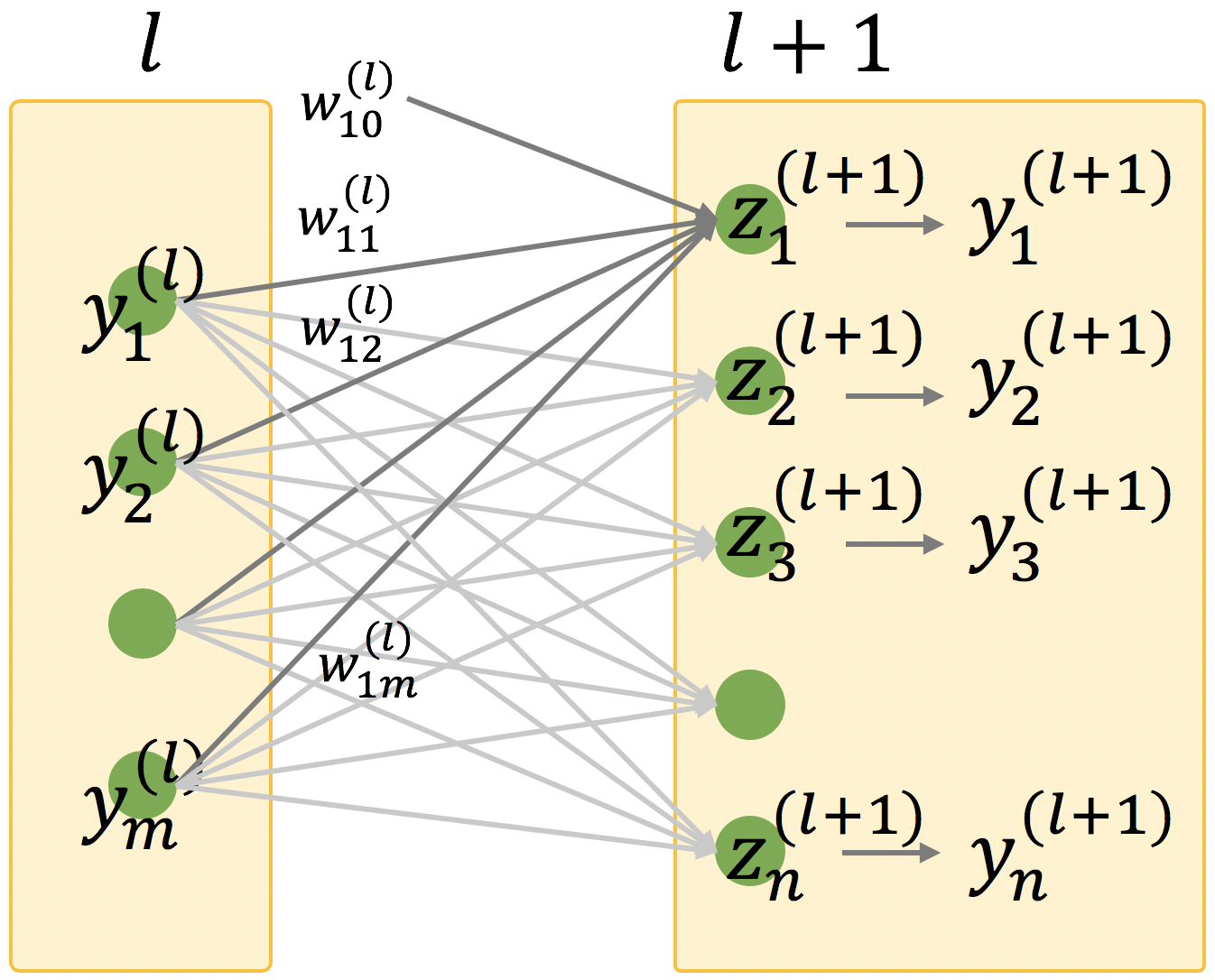
ここでウェイト w をベクトルで表すと、
\[ \mathbf{w} = \begin{pmatrix} w_{11} & w_{12} & \cdots & w_{1m} \\ w_{21} & w_{22} & \cdots & w_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n1} & w_{n2} & \cdots & w_{nm} \\ \end{pmatrix} \]l 層目から l+1 層目への情報の受け渡しは次のように計算することができる。
\[ \begin{pmatrix} y^{(l+1)}_{1} \\ y^{(l+1)}_{2} \\ \vdots \\ y^{(l+1)}_{n} \end{pmatrix} = \begin{pmatrix} w^{(l)}_{10} \\ w^{(l)}_{20} \\ \vdots \\ w^{(l)}_{n0} \end{pmatrix} + \left( \begin{pmatrix} w_{11} & w_{12} & \cdots & w_{1m} \\ w_{21} & w_{22} & \cdots & w_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n1} & w_{n2} & \cdots & w_{nm} \\ \end{pmatrix} \begin{pmatrix} y^{(l)}_{1} \\ y^{(l)}_{2} \\ \vdots \\ y^{(l)}_{m} \end{pmatrix} \right)^{T} \]これをベクトルで表記すると次のようになる。
\[ \mathbf{z}^{(l+1)} = \mathbf{w}^{(l)}_{0} + \left(\mathbf{w}^{(l)}\mathbf{y}^{(l)}\right)^{T} \] \[ \mathbf{y}^{(l+1)} = f(\mathbf{z}^{(l+1)}) \]順伝播型ニューラルネットワークは、このように入力層から第 1 層目の中間層に情報を渡し、第 1 層目のユニットの計算結果を第 2 層目のユニットに渡し、・・・、のように情報を 1 層ずつ隣接する層に伝えていくニューラルネットワークである。