畳み込みニューラルネットワークは物体認識(物体分類)の分野で大きな成功を納めているものの、各層のパラメーター同士の繋がりが複雑で、解釈性に欠けている。畳み込みニューラルネットワークが、写真のどこを見て、何をもって物体認識を行っているのを解明することで、畳み込みニューラルネットワークのさらなる改良に繋がるだけでなく、ユーザーが安心して使えるものになる。畳み込みニューラルネットワークの各層を可視化して解釈できるようにする研究が多く行われている。そのなかで、比較的による知られているのが Grad-CAM である。Grad-CAM を理解するには、global average pooling (GAP) および class activation map (CAM) についても理解する必要がある。
global average pooling (GAP)
一般的な畳み込みニューラルネットワークは、下図左のにょうに、畳み込み層の出力値をそのまま分類用のニューラルネットワークに代入している。これに対して、global average pooling (GAP) は、各特徴量マップ(チャンネル)ごとの平均値を計算し、その平均値を後続のニューラルネットワークに代入している。
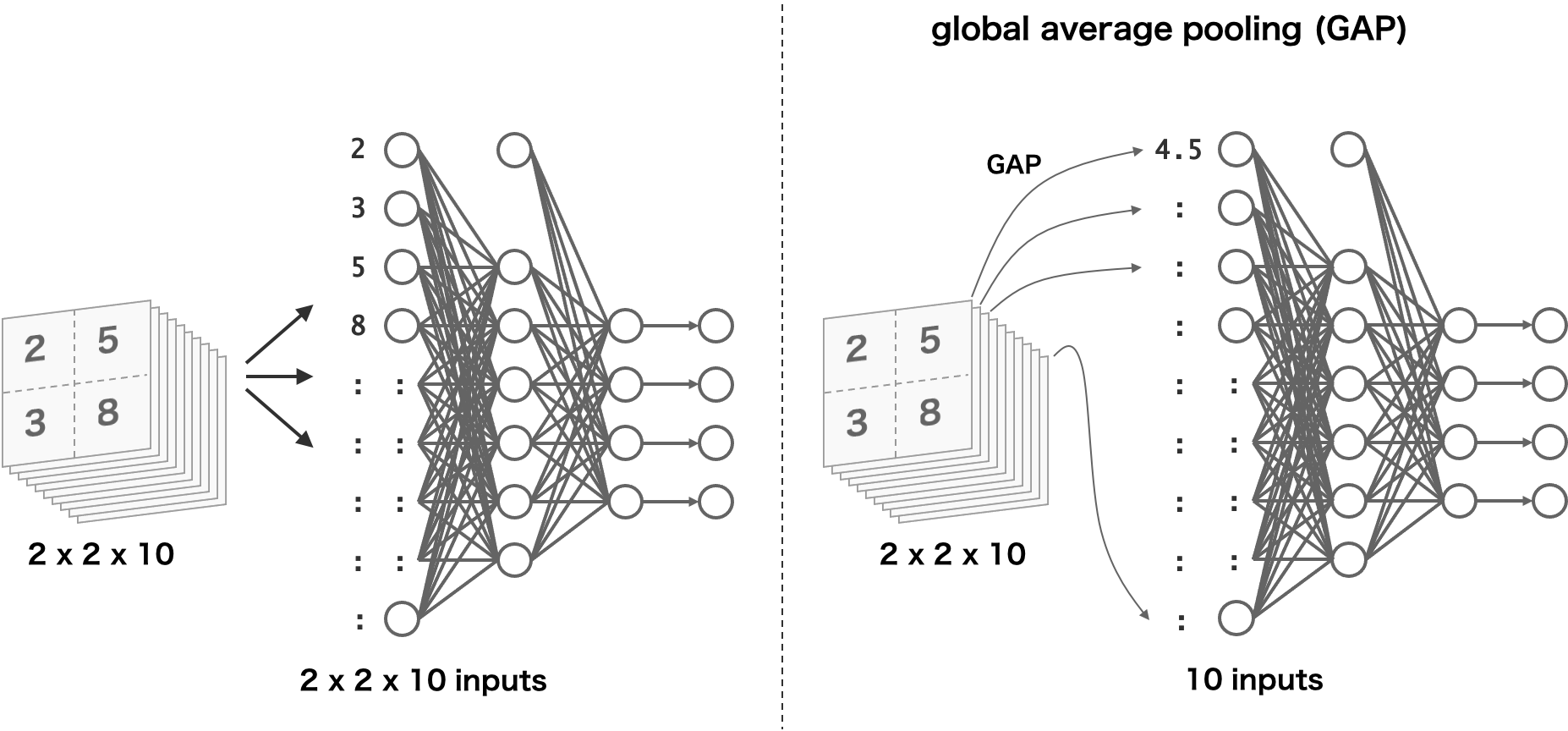
畳み込み層の出力値をそのままニューラルネットワークに代入すると、ニューラルネットワークの入力層には多くのユニットを用意する必要しておく必要がある。例えば、上図の例では、入力層には 2×2×10 = 400 個のユニットを用意する必要がある。これに対して、GAP の場合は、特徴量マップごとに平均値を求めて、その平均値を次のニューラルネットワークに入力している。そのため、ニューラルネットワークの入力層は、畳み込み層が出力した特徴量マップの数になる。上図の例では、10 である。このように、畳み込み演算を行った結果に対して GAP を行い、その結果を後続のニューラルネットワークに代入することにより、パラメータの数を大幅に削減できる。
Class activation map (CAM)
Class activation map (CAM) は、畳み込みニューラルネットワークが物体を認識する際に、画像をどこに着目しているのかを可視化する方法である。CAM は、GAP の結果(分類用ニューラルネットワークの入力)と予測結果の間にある重みに着目して、可視化を行っている。CAM の概要を理解する上で次の図が使われる(Zhou et al.)。
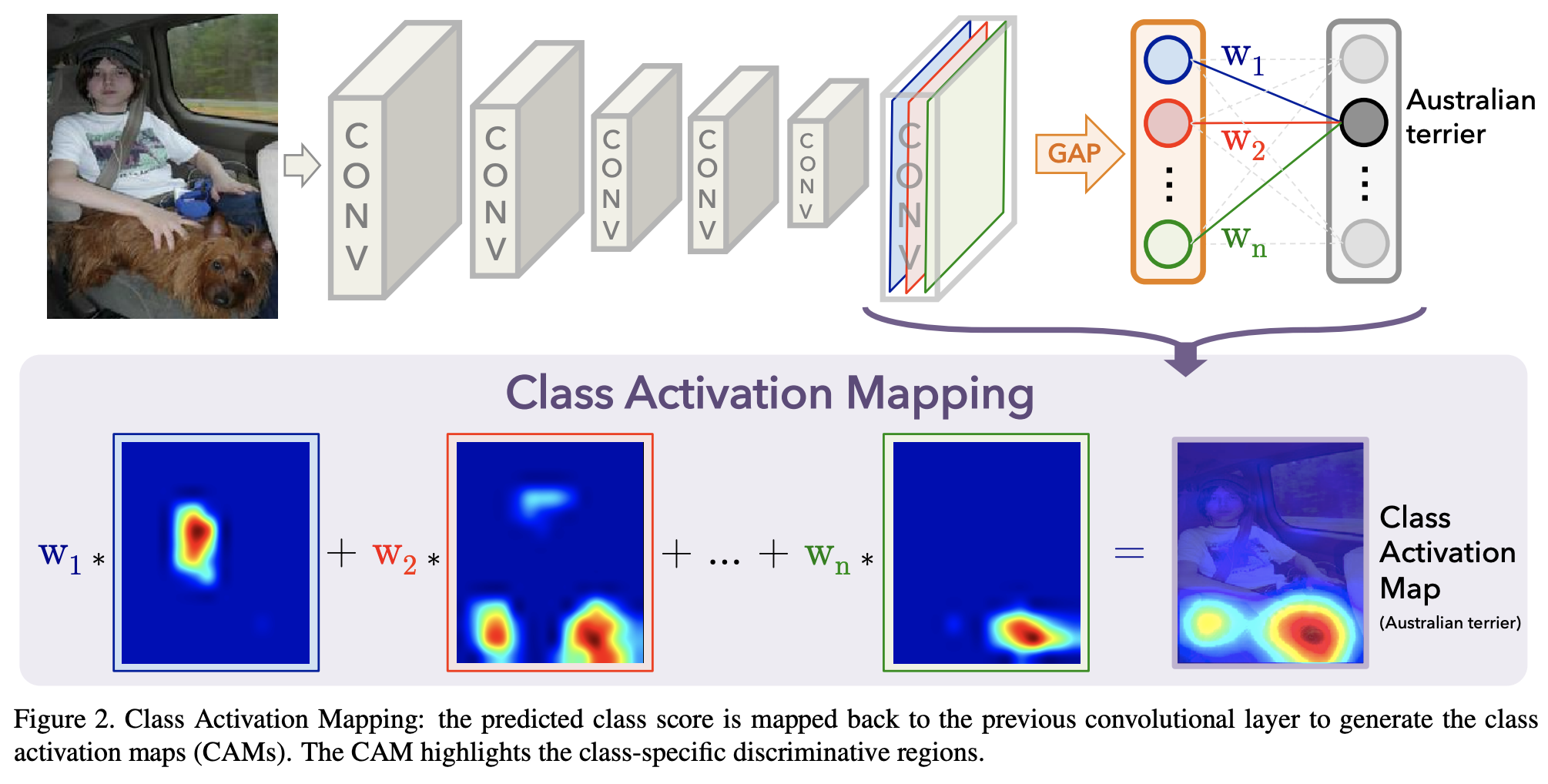
GAP は、畳み込み層の出力した特徴量マップごとに平均を計算して、後続のニューラルネットワークに入力している。そして後続のニューラルネットワークでは、GAP の計算結果に対して重みを計算して、最終的な出力値を計算している。そこで、出力層からみて、例えば上図のように「Australian terrier」のユニットの出力値に着目したときに、この出力値は、GAP の計算結果に対して重み w1, w2, ..., wn をかけて、その線形結合で計算される。ここで、例えば、w1 は大きな値で、w2 がゼロに近い非常に小さい値であるとします。ここから、GAP 計算結果のうち、最初の値は Austrilian terrier の判別にとって非常に重要で、2 番目の値はほとんど役に立たない、ということが考えられる。GAP の計算元を考慮すると、最初の特徴マップが Austrilian terrier の判別に重要で、2 番目の特徴マップはほとんど役に立っていないということになる。このような考えのもとで、すべての特徴マップについて考えていくと、結局、回帰分析のように、各特徴マップに重みをかけて、重ね合わせたものが、Austrilian terrier の判別根拠になると考えられる。
このように、CAM は最後の畳み込み層が出力した特徴量マップに重みをかけて、判断根拠を可視化する方法である。これを数式化して考えていく。fk(x, y) を k 番目の特徴量マップの座標 (x, y) の出力とする。k 番目の特徴量マップに対して GAP を行った結果を Fk とすると、Fk は次のように書ける。
\[ F_{k} = \sum_{x, y}f_{k}(x,y) \]次に、GAP 結果をニューラルネットワークに代入し計算を行う。ニューラルネットワークのカテゴリ c の出力値 Sc は、出力ユニット c と k 番目の 入力値(GAP 結果)の間を結ぶ重み wkc を用いると、次のように計算できる。ここで計算される Sc は、必要に応じてソフトマックス関数に代入して、カテゴリ c になる確率を計算することができる。
\[ \begin{eqnarray} S_{c} &=& \sum_{k}w_{k}^{c}F_{k} \\ &=& \sum_{k}w_{k}^{c}\sum_{x, y}f_{k}(x,y) = \sum_{x, y}\sum_{k}w_{k}^{c}f_{k}(x,y) \end{eqnarray} \]この式をみると、上で説明した CAM の計算は \( \sum_{k}w_{k}^{c}f_{k}(x,y) \) の部分にあたる。そこで、
\[ M_{c}(x,y) = \sum_{k}w_{k}^{c}f_{k}(x,y) \]とおく。このとき、ニューラルネットワークのカテゴリ c の出力値は、
\[ S_{c} = \sum_{x, y} M_{c}(x,y) \]とかける。この式から、ニューラルネットワークのカテゴリ c の出力値は、Mc そのものに影響される。つまり、Mc こそがカテゴリ c の判断根拠となる。
Grad-CAM
Grad-CAM (Selvaraju et al.) は、CAM を拡張した可視化法である。CAM では、GAP 計算値とニューラルネットワーク出力層の間を結ぶ重みを特徴量マップにかけて、画像中の判断根拠となる部位を可視化している。これに対して、Grad-CAM は、重みの部分を、逆伝播時の勾配で代用する方法である。これにより、GAP を含まない畳み込みニューラルネットワークのアーキテクチャでも判断根拠を可視化できるようになる。

カテゴリ c における Grad-CAM は、次のように計算される。
\[ L_{c} = ReLU \left( \sum_{k} \alpha_{k}^{c} f_{k}(x, y) \right) \]重み α は、次のように勾配から計算する。ただし、Z は規格化定数で、\(Z = \sum_{x, y}1\) である。
\[ \alpha_{k}^{c} = \frac{1}{Z}\sum_{x, y} \frac{\partial S_{c}}{\partial f_{k}(x, y)} \]\( \frac{\partial S_{c}}{\partial f_{k}(x, y)} \) は、特徴量マップ k の座標 (x, y) の画素が変化したとき、ニューラルネットワークのカテゴリ c の出力値 Sc がどのぐらい変化するのかを表している。\( \frac{\partial S_{c}}{\partial f_{k}(x, y)} \) の値が大きいということは、特徴量マップの座標 (x, y) の部分が少しだけしか変化していないにもかかわらず、カテゴリ c の出力値 Sc が大きく変化してしまう、ということを意味する。すなわち、座標 (x, y) が、カテゴリ c を認識する上で非常に重要な部分であることがわかる。
このように、Grad-CAM は、特徴量マップからニューラルネットワークの出力値の間の勾配を利用して、判断根拠を可視化している。
Guided Grad-CAM
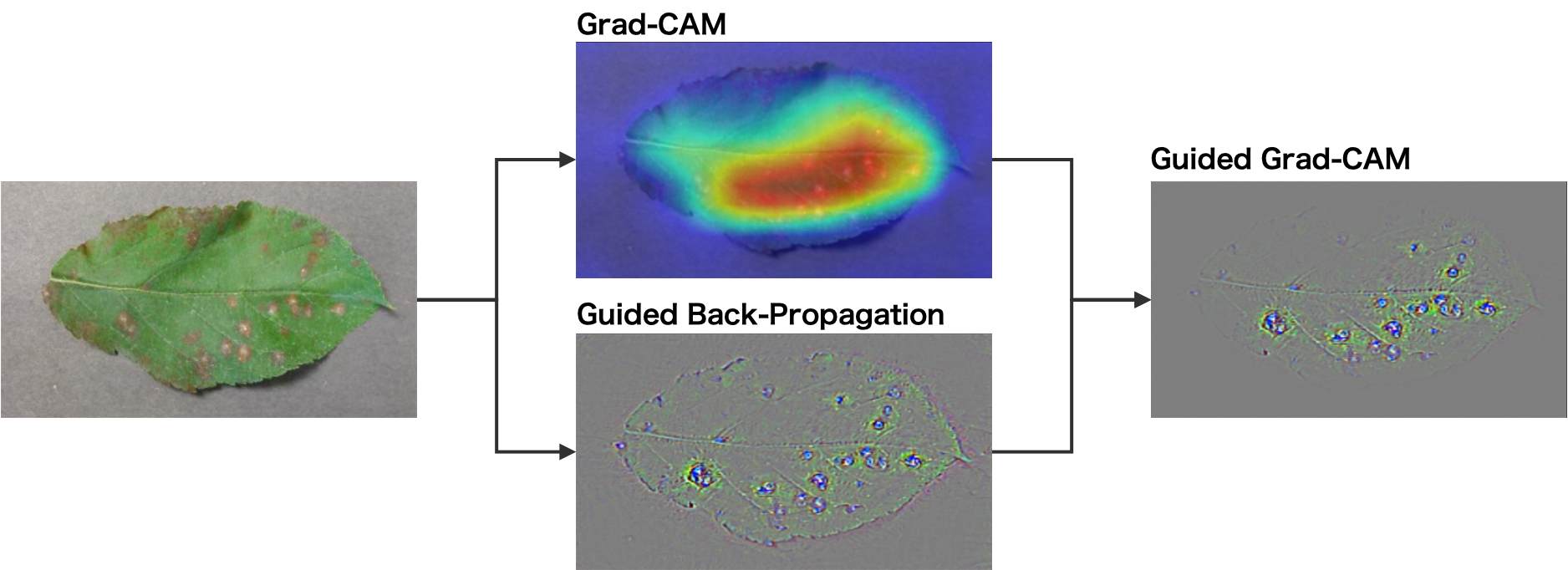
畳み込みニューラルネットワークの判断根拠の可視化方法には guided backpropagation というものもある。この guided backpropagation による可視化と grad-CAM による可視化を重ねたものを guided Grad-CAM とよぶ。
References
- Learning Deep Features for Discriminative Localization. arxiv 2015, 1512.04150. arxiv: 1512.04150
- Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization. arxiv 2016, 1610.02391. arxiv: 1610.02391
- 2019年までのCAM(Class Activation Map)まとめ. Qiita