1×1 Convolution は、入力画像のサイズを変えずに、チャンネルの数を変更する畳み込み操作である（Lin et al., 2014）。チャンネル数を減らすことで、求めるべきパラメーター数が減り、次元削減の効果が現れる。1×1 Convolution は、GoogLeNet などで、チャンネル数を減らすために使われている。

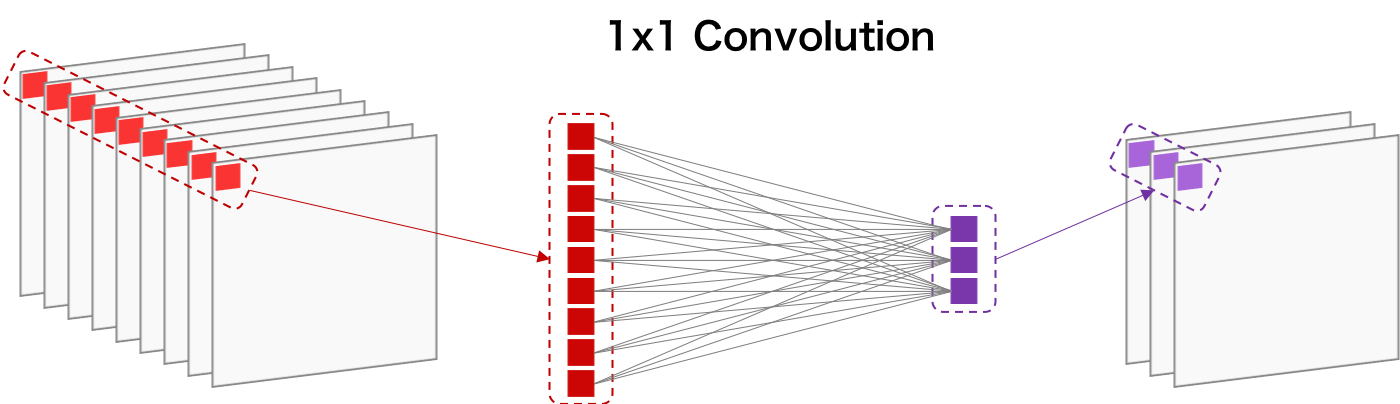
次元削減を説明するために、ここで、サイズが 14×14×480 のデータを考える。このデータに対して 5×5 のフィルターで畳み込みを行って、 14×14×48 のデータに変換させたとき、 畳み込み計算は 112,896,000 回行われることになる。

これに対して、5×5 による畳み込み計算を行う前に、1×1 Convolution でチャンネル数を減らせば、畳み込み計算の回数を減らすことができる。例えば、もともと 480 チャンネルを 1×1 Convolution で 16 チャンネル数に減らしたあとに、5×5 による畳み込みを行う場合は、畳み込み計算は合計で 1,505,280 + 3,763,200 = 5,268,480 回行われることになる。

1×1 Convolution を利用したときとそうでない時の計算回数を比べると、後者は前者よりも 112,896,000 - 5,268,480 = 107,627,520 回も計算数が少ない。このように、入力画像に対して直接畳み込み計算を行うよりも、1×1 Convolution を行ってから畳み込み計算を行うことで、パラメーターの次元数を減らすことができ、過学習を減らすことができる。