活性化関数は、前のニューロンから送られた複数の値に重みをかけ、その総和を 1 つの値として出力する関数である。ステップ関数、シグモイド関数や ReLU 関数がなどが活性化関数としてよく用いられる。

恒等関数

恒等関数は入力された値をそのまま返す関数である。主に回帰問題の出力層の活性化関数として使われる。式で表すと次のようになる。

ステップ関数

ステップ関数は、入力された値が、ある閾値を超えた時に 1 を出力し、それ以外の閾値以下の場合は 0 を出力する関数である。入力値を x、閾値を θ とすると、ステップ関数は次の式で表すことができる。

ステップ関数を Python で実装すると、次のようになる。次の例では閾値を 0 としている。

def step_function(x):
    if x < 0:
        return 1
    else:
        return 0

複数の入力値を（それぞれ独立に）いっぺんに判断する際に、numpy ライブラリーのベクトル型（配列型）を利用する。

import numpy as np

def step_function(x):
    x = np.array(x)
    v = x < 0
    y = x.astype(np.int)
    return y

ReLU 関数

ReLU (rectified linear unit) 関数は、入力値が 0 以下ならば 0 を出力し、入力値が 0 よりも大きければそのまま出力する関数である。ReLU 関数は非線形変換を行う関数であり、その関数の形から微分で勾配が消えにくい。そのため、ReLU 関数はニューラルネットワークの中間層の活性化関数としてよく使われている。

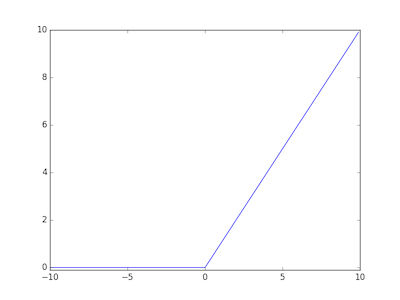
Python で実装すると次のようになる。

import numpy as np

def relu_function(x):
    return np.maximum(0, x)

シグモイド関数

シグモイド関数は、マイナスの無限大からプラスの無限大までの値を受け取り、それを 0 から 1 までの範囲の値に変換して出力している非線形関数である。出力値の範囲に着目すれば、シグモイド関数が入力値を確率に変換していると言える。分類問題では、最後にどのクラスが確率何パーセントなのか、という確率で出力することが多いことから、シグモイド関数は、分類問題のニューラルネットワークの出力層の活性化関数として使われることが多い。

出力層の活性化関数として、シグモイド関数のほかに、ソフトマックス関数や恒等関数などがよく使われる。回帰問題のときは恒等関数を使い、分類問題のときはシグモイド関数またはソフトマックス関数を使用する。シグモイド関数とソフトマックス関数の両方とも多クラス分類問題に使用できる。ノートパソコンが写っている写真を分類したとき、「パソコン 90%; キーボード 80%; ディスプレイ 80%; 猫 0%; ...」のようなクラスワイズな分類結果を期待するときにシグモイド関数を使う。また、「パソコン 90%; キーボード 5%; ディスプレイ 5%; 猫 0%; ...」のような合計 100% になる分類結果を期待する場合は、ソフトマックス関数を使う。

シグモイド関数は次のように書ける。

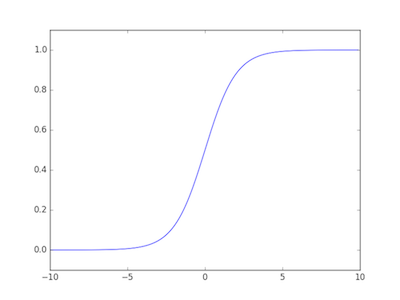
Python で実装すると次のようになる。

import numpy as np

def sigmoid_function(x):
    return 1 / (1 + np.exp(-x))

ソフトマックス関数

シグモイド関数は、一つの値を受け取り、一つの 0 から 1 まで範囲にある値を出力する関数である。これに対して、ソフトマックス関数は、一つのベクトルを受け取り、一つのベクトルを出力する関数である。ソフトマックス関数で出力されるベクトルの和が 1.0 になる。ソフトマックス関数は、複数の値からなる入力ベクトルをすべて合計 1.0 となるよう出力ベクトルに変換しているため、多クラスの分類問題の出力層でよく使われている。

入力ベクトルを x = (x₁, x₂, ..., x_n) とし、出力ベクトルを y = (y₁, y₂, ..., y_n) とすると、ソフトマックス関数は次の式で書き表すことができる。

ソフトマックス関数を Python で実装すると次のようになる。

import numpy as np

def softmax_function(x):
    z = np.exp(x)
    return z / np.sum(z)